
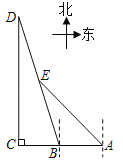
【题目】如图,为某景区五个景点A、B、C、D、E的平面示意图,B、A在C的正东方向,D在C的正北方向,D和E均在B的北偏西18°方向上,E在A的西北方向上,C、D相距1000米,E在BD的中点处,求景点B、A之间的距离.(结果保留整数)
(参考数据:sin18°≈0.3;cos18°≈0.9;tan18°≈0.3;sin72°≈0.9;cos72°≈0.3;tan72°≈3.1;![]() ≈1.4)
≈1.4)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线y=kx+1与x轴、y轴分别相交于点A、B,将△AOB绕点A顺时针旋转,使AO落在AB上,得到△ACD,将△ACD沿射线BA平移,当点D到达x轴时运动停止.设平移距离为m,平移后的图形在x轴下方部分的面积为S,S关于m的函数图象如图2所示(其中0<m≤2,2<m≤a时,函数的解析式不同)
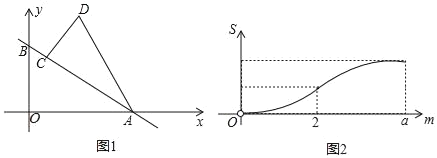
(1)填空:a= ,k= ;
(2)求S关于m的解析式,并写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴相交于点
轴相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() ,
,![]() .
.
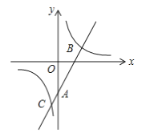
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形,如果存在,请求点
为等腰三角形,如果存在,请求点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为顶点,连接
为顶点,连接![]() ,
,![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交与点
轴交与点![]() .
.
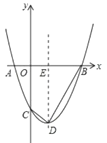
(1)求抛物线解析式及点![]() 的坐标;
的坐标;
(2)G是抛物线上![]() ,
,![]() 之间的一点,且
之间的一点,且![]() ,求出
,求出![]() 点坐标;
点坐标;
(3)在抛物线上![]() ,
,![]() 之间是否存在一点
之间是否存在一点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出满足条件的点
相似?若存在,求出满足条件的点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
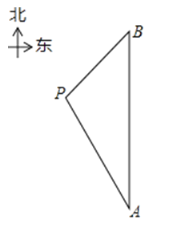
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月18日,《感动中国2018年度人物颁奖盛典》在央视综合频道播出,其中乡村教师张玉滚的事迹令人非常感动某校团委组织“支援乡村教育,帮助教师张玉滚”的捐款活动,以下为九年级(1)班捐款情况:
捐款金额(元) | 5 | 10 | 20 | 50 |
人数(人) | 12 | 13 | 16 | 11 |
则这个班学生捐款金额的中位数和众数分别为( )
A.15,50B.20,20C.10,20D.20,50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 中,AB=8,BC=6,将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG,AE,FG 分别交射线CD 于点 PH,连结 AH,若 P 是 CH 的中点,则△APH 的周长为( )
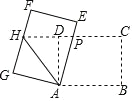
A. 15 B. 18 C. 20 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
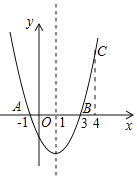
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
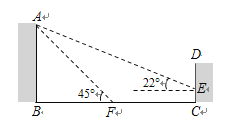
【题目】(满分8分)如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C的距离为18m (B、F、C在一条直线上).
求教学楼AB的高度.(结果保留整数)
(参考数据:sin22°![]() 0.37,cos22°
0.37,cos22°![]() 0.93,tan22°
0.93,tan22°![]() 0.40 .)
0.40 .)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com