
【题目】如图,已知:抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为顶点,连接
为顶点,连接![]() ,
,![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交与点
轴交与点![]() .
.
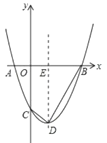
(1)求抛物线解析式及点![]() 的坐标;
的坐标;
(2)G是抛物线上![]() ,
,![]() 之间的一点,且
之间的一点,且![]() ,求出
,求出![]() 点坐标;
点坐标;
(3)在抛物线上![]() ,
,![]() 之间是否存在一点
之间是否存在一点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出满足条件的点
相似?若存在,求出满足条件的点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]() ;顶点
;顶点![]() 坐标为
坐标为![]() ;(2)点
;(2)点![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)由点A、B坐标即可得到抛物线的解析式,将![]() 配成顶点式即可求出顶点;
配成顶点式即可求出顶点;
(2)设![]() ,待定系数法求出直线BC的解析式,求出DF,得到△BCD的面积,根据
,待定系数法求出直线BC的解析式,求出DF,得到△BCD的面积,根据![]() ,得到
,得到![]() ,待定系数法求出BD解析式,从而表达出△BDG的面积,列出方程即可解答;
,待定系数法求出BD解析式,从而表达出△BDG的面积,列出方程即可解答;
(3)以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,则以
相似,则以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,①当△PCB∽△BDE,②当△CPB∽△BDE,利用相似比解出BP,求出点P坐标及直线CP的解析式,联立方程组即可求出M的坐标.
相似,①当△PCB∽△BDE,②当△CPB∽△BDE,利用相似比解出BP,求出点P坐标及直线CP的解析式,联立方程组即可求出M的坐标.
解:(1)∵抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,
∴![]() ,
,
解得![]() .
.
所以,抛物线的解析式为![]() ;
;
∴![]() ;
;
∴顶点![]() 坐标为
坐标为![]() .
.
(2)连接![]() ,
,
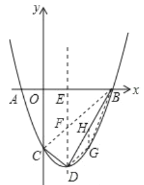
令![]() ,则
,则![]() ,
,
所以,点![]() ,
,
设直线BC的解析式为y=ax+d,
将![]() ,
,![]() 代入得
代入得![]() ,解得a=1,d=-3;
,解得a=1,d=-3;
∴直线![]() 的解析式为
的解析式为![]() ,
,
设直线![]() 与对称轴相交于点
与对称轴相交于点![]() ,
,
![]() 时,
时,![]() ,
,
所以,点![]() ,
,
所以,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
设过点![]() 与
与![]() 轴平行的直线相交于点
轴平行的直线相交于点![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,
解得![]() ,
,
所以,直线![]() 的解析式为
的解析式为![]() ,
,
设![]() ,
,
则![]() ,
,
所以,![]() ,
,
整理得,![]() ,
,
解得![]() ,
,
![]() ,
,
所以,点![]() ;
;
(3)存在
由勾股定理得,![]() ,
,
如图,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 、
、![]() 与
与![]() 轴的夹角都是45°,
轴的夹角都是45°,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,
∴以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,
①当△PCB∽△BDE
∴![]() ,即
,即![]()
解得![]() ,
,
∴![]() ,
,
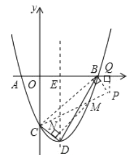
所以,![]() ,
,
所以,点![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则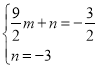 ,
,
解得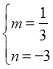 ,
,
所以,直线![]() 的解析式为
的解析式为![]() ,
,
联立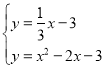 ,
,
解得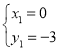 (舍去),
(舍去),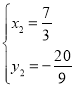 ,
,
所以,点![]() ,
,
②当△CPB∽△BDE
∴![]() ,即
,即![]()
解得![]() ,
,
∴![]() ,
,
所以,![]() ,
,
所以,点![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,
解得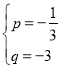 ,
,
所以,直线![]() 的解析式为
的解析式为![]() ,
,
联立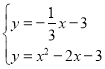 ,
,
解得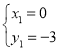 (舍去),
(舍去),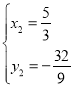 ,
,
∴点![]() ,
,
综上所述,存在点![]() 或
或![]() ,使
,使![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】工程队在完成某项工程的过程中,因提高了工作效率从而缩短了工作时间.经测试:工作时间缩短的百分率是工作效率提高的百分率的2倍,且提高工作效率后的工作量是原来工作量的0.88倍.若完成原来工作量的时间为3小时,求提高工作效率后完成工作量所花的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
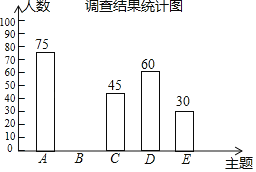
【题目】2019年3月19日,河南省教育厅发布《关于推进中小学生研学旅行的实施方案》,某中学为落实方案,给学生提供了以下五种主题式研学线路:A.“红色河南”,B.“厚重河南”C.“出彩河南”,D.“生态河南”,E.“老家河南”为了解学生最喜欢哪一种研学线路(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:
调查结果统计表
主题 | 人数/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受调查的总人数为 人,统计表中m= ,n= .
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则“生态河南”主题线路所在扇形的圆心角度是 .
(4)若该实验中学共有学生3000人,请据此估计该校最喜欢“老家河南”主题线路的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() ;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
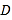
查看答案和解析>>
科目:初中数学 来源: 题型:
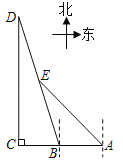
【题目】如图,为某景区五个景点A、B、C、D、E的平面示意图,B、A在C的正东方向,D在C的正北方向,D和E均在B的北偏西18°方向上,E在A的西北方向上,C、D相距1000米,E在BD的中点处,求景点B、A之间的距离.(结果保留整数)
(参考数据:sin18°≈0.3;cos18°≈0.9;tan18°≈0.3;sin72°≈0.9;cos72°≈0.3;tan72°≈3.1;![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
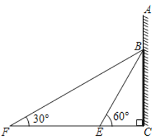
【题目】如图,在某建筑物AC上,挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行30米到达点E处,看到条幅顶端B,测得仰角为60°,求宣传条幅BC的长.(注:不计小明的身高,结果精确到1米,参考数据![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
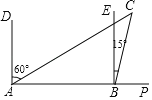
【题目】如图,一游船往返于A,B,C三岛,此船从A岛出发向正东方向航行1小时到达B岛,C岛在A岛的北偏东60°方向,在B岛的北偏东15°方向,已知游船的航速为20海里/小时,求此船从B岛航行到C岛需要多少小时?(![]() ≈1.414,结果精确到0.1小时)
≈1.414,结果精确到0.1小时)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com