
【题目】工程队在完成某项工程的过程中,因提高了工作效率从而缩短了工作时间.经测试:工作时间缩短的百分率是工作效率提高的百分率的2倍,且提高工作效率后的工作量是原来工作量的0.88倍.若完成原来工作量的时间为3小时,求提高工作效率后完成工作量所花的时间.
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
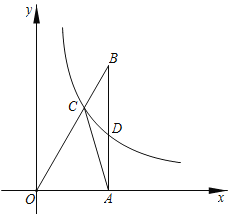
【题目】如图,在平面直角坐标系xOy中,Rt△OAB的直角顶点A在x轴上,∠B=30°,反比例函数y=![]() (k≠0)在第一象限的图象经过OB边上的点C和AB的中点D,连接AC.已知S△OAC=4
(k≠0)在第一象限的图象经过OB边上的点C和AB的中点D,连接AC.已知S△OAC=4![]() ,则实数k的值为( )
,则实数k的值为( )
A.4![]() B.6
B.6![]() C.8
C.8![]() D.10
D.10![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系![]() 中,双曲线
中,双曲线![]()
![]() 与直线
与直线![]()
![]() 交于
交于![]() 、
、![]() 两点,直线
两点,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 轴上一点.已知
轴上一点.已知![]() ,
,![]() 点坐标为
点坐标为![]() .
.
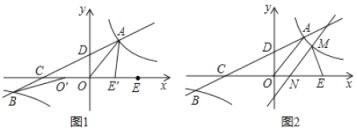
(1)将线段![]() 沿
沿![]() 轴平移得线段
轴平移得线段![]() (如图1),在移动过程中,是否存在某个位置使
(如图1),在移动过程中,是否存在某个位置使![]() 的值最大?若存在,求出
的值最大?若存在,求出![]() 的最大值及此时点
的最大值及此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
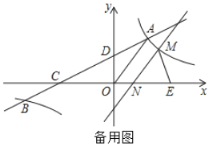
(2)将直线![]() 沿射线
沿射线![]() 平移,平移过程中交
平移,平移过程中交![]()
![]() 的图象于点
的图象于点![]() (
(![]() 不与
不与![]() 重合),交
重合),交![]() 轴于点
轴于点![]() (如图2).在平移过程中,是否存在某个位置使
(如图2).在平移过程中,是否存在某个位置使![]() 为以
为以![]() 为腰的等腰三角形?若存在,求出
为腰的等腰三角形?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二十四届冬季奧林匹克运动会将于2022年2月4日至2月20日在北京举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有![]() 名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
[收集数据]
从甲、乙两校各随机抽取![]() 名学生,在这次竞赛中他们的成绩如下:
名学生,在这次竞赛中他们的成绩如下:
甲:![]()
![]()
乙:![]()
![]()
[整理、描述数据]按如下分数段整理、描述这两组样本数据:
学校 人数 成绩 |
|
|
|
甲 |
|
|
|
乙 |
|
|
|
(说明:优秀成绩为![]() ,良好成绩为
,良好成绩为![]() 合格成绩为
合格成绩为![]() .)
.)
[分析数据]两组样本数据的平均分、中位数、众数如下表所示:
学校 | 平均分 | 中位数 | 众数 |
甲 |
|
|
|
乙 |
|
|
|
其中![]() .
.
[得出结论]
(1)小明同学说:“这次竞赛我得了![]() 分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
(2)张老师从乙校随机抽取--名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为_ ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由: ;
(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
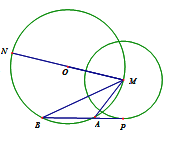
【题目】如图,⊙O是以MN为直径,半径为4的圆,P为以M为圆心、2为半径的圆上一点,过点P作⊙M的切线交⊙O于点A.B,连MA,MB,则MA·MB为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为改善生态环境,实行生活垃圾的分类处理,将生活垃圾分成三类:厨房垃圾、可回收垃圾和其他垃圾,分别记为![]() ,并且设置了相应的垃圾箱“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为
,并且设置了相应的垃圾箱“厨房垃圾”箱,“可回收垃圾”箱和“其他垃圾”箱,分别记为![]() .
.
(1)为了了解居民生活垃圾分类投放的情况,现随机抽取了小区三类垃圾箱中总共![]() 吨生活垃圾,数据统计如下图(单位:吨):
吨生活垃圾,数据统计如下图(单位:吨):
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
请根据以上信息,估计“厨房垃圾”投放正确的概率;
(2)若将三类垃圾随机投入三类垃圾箱,请用画树状图或列表格的方法求出垃圾投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=kx+1与x轴、y轴分别相交于点A、B,将△AOB绕点A顺时针旋转,使AO落在AB上,得到△ACD,将△ACD沿射线BA平移,当点D到达x轴时运动停止.设平移距离为m,平移后的图形在x轴下方部分的面积为S,S关于m的函数图象如图2所示(其中0<m≤2,2<m≤a时,函数的解析式不同)
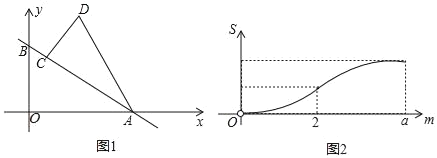
(1)填空:a= ,k= ;
(2)求S关于m的解析式,并写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为顶点,连接
为顶点,连接![]() ,
,![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交与点
轴交与点![]() .
.
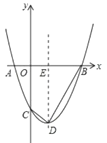
(1)求抛物线解析式及点![]() 的坐标;
的坐标;
(2)G是抛物线上![]() ,
,![]() 之间的一点,且
之间的一点,且![]() ,求出
,求出![]() 点坐标;
点坐标;
(3)在抛物线上![]() ,
,![]() 之间是否存在一点
之间是否存在一点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出满足条件的点
相似?若存在,求出满足条件的点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com