
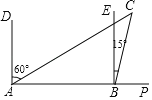
【题目】如图,一游船往返于A,B,C三岛,此船从A岛出发向正东方向航行1小时到达B岛,C岛在A岛的北偏东60°方向,在B岛的北偏东15°方向,已知游船的航速为20海里/小时,求此船从B岛航行到C岛需要多少小时?(![]() ≈1.414,结果精确到0.1小时)
≈1.414,结果精确到0.1小时)
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为顶点,连接
为顶点,连接![]() ,
,![]() ,抛物线的对称轴与
,抛物线的对称轴与![]() 轴交与点
轴交与点![]() .
.
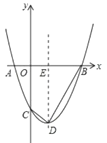
(1)求抛物线解析式及点![]() 的坐标;
的坐标;
(2)G是抛物线上![]() ,
,![]() 之间的一点,且
之间的一点,且![]() ,求出
,求出![]() 点坐标;
点坐标;
(3)在抛物线上![]() ,
,![]() 之间是否存在一点
之间是否存在一点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,使以
,使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出满足条件的点
相似?若存在,求出满足条件的点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
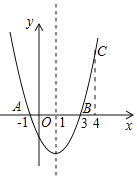
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
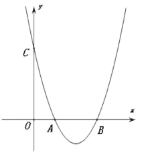
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(3)在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
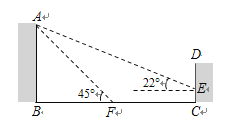
【题目】(满分8分)如图,某教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C的距离为18m (B、F、C在一条直线上).
求教学楼AB的高度.(结果保留整数)
(参考数据:sin22°![]() 0.37,cos22°
0.37,cos22°![]() 0.93,tan22°
0.93,tan22°![]() 0.40 .)
0.40 .)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=10cm,E为对角线BD上一动点,连接AE,CE,过E点作EF⊥AE,交直线BC于点F.E点从B点出发,沿着BD方向以每秒2cm的速度运动,当点E与点D重合时,运动停止.设△BEF的面积为ycm2,E点的运动时间为x秒.
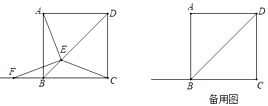
(1)求证:CE=EF;
(2)求y与x之间关系的函数表达式,并写出自变量x的取值范围;
(3)求△BEF面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() +b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
+b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量x的取值范围;
(2)请在下列直角坐标系中画出该函数的图象;
(3)请你在上方直角坐标系中画出函数y=2x的图象,结合上述函数的图象,写出不等式![]() +b≤2x的解集.
+b≤2x的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com