
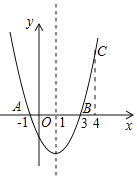
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
【答案】①④
【解析】
利用交点式写出抛物线解析式为y=ax2﹣2ax﹣3a,配成顶点式得y=a(x﹣1)2﹣4a,则可对①进行判断;计算x=4时,y=a51=5a,则根据二次函数的性质可对②进行判断;利用对称性和二次函数的性质可对③进行判断;由于b=﹣2a,c=﹣3a,则方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0,然后解方程可对④进行判断.
解:∵二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0),
∴抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∵y=a(x﹣1)2﹣4a,
∴当x=1时,二次函数有最小值﹣4a,所以①正确;
当x=4时,y=a51=5a,
∴当﹣1≤x2≤4,则﹣4a≤y2≤5a,所以②错误;
∵点C(4,5a)关于直线x=1的对称点为(﹣2,5a),
∴当y2>y1,则x2>4或x<﹣2,所以③错误;
∵b=﹣2a,c=﹣3a,
∴方程cx2+bx+a=0化为﹣3ax2﹣2ax+a=0,
整理得3x2+2x﹣1=0,解得x1=﹣1,x2=![]() ,所以④正确.
,所以④正确.
故答案为①④.


科目:初中数学 来源: 题型:
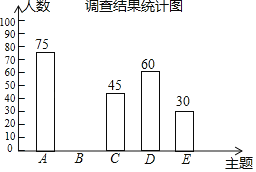
【题目】2019年3月19日,河南省教育厅发布《关于推进中小学生研学旅行的实施方案》,某中学为落实方案,给学生提供了以下五种主题式研学线路:A.“红色河南”,B.“厚重河南”C.“出彩河南”,D.“生态河南”,E.“老家河南”为了解学生最喜欢哪一种研学线路(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:
调查结果统计表
主题 | 人数/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受调查的总人数为 人,统计表中m= ,n= .
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则“生态河南”主题线路所在扇形的圆心角度是 .
(4)若该实验中学共有学生3000人,请据此估计该校最喜欢“老家河南”主题线路的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
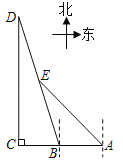
【题目】如图,为某景区五个景点A、B、C、D、E的平面示意图,B、A在C的正东方向,D在C的正北方向,D和E均在B的北偏西18°方向上,E在A的西北方向上,C、D相距1000米,E在BD的中点处,求景点B、A之间的距离.(结果保留整数)
(参考数据:sin18°≈0.3;cos18°≈0.9;tan18°≈0.3;sin72°≈0.9;cos72°≈0.3;tan72°≈3.1;![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
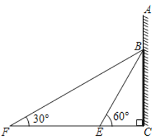
【题目】如图,在某建筑物AC上,挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行30米到达点E处,看到条幅顶端B,测得仰角为60°,求宣传条幅BC的长.(注:不计小明的身高,结果精确到1米,参考数据![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中.

(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标;
三个顶点的坐标;
(2)直接写出△ABC的面积为 ;
(3)在x轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
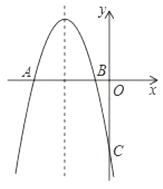
【题目】如图所示,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,![]() ,与
,与![]() 轴交于
轴交于![]() ,并且对称轴
,并且对称轴![]() .
.

(1)求抛物线的解析式;
(2)![]() 在
在![]() 轴上方的抛物线上,过
轴上方的抛物线上,过![]() 的直线
的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)点![]() 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当![]() 是以
是以![]() 为直角边的直角三角形时,求
为直角边的直角三角形时,求![]() 点坐标;
点坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … | - | 0 |
| 1 |
| 2 |
| … |
y | … |
| -1 | - | m | - | -1 | n | … |
则对于该函数的性质的判断:
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;
③方程ax2+bx+c=0的两个实数根分别位于-![]() <x<0和2<x<
<x<0和2<x<![]() 之间;
之间;
④当x>0时,函数值y随x的增大而增大;
其中正确的是:
A.②③B.②④C.①③D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
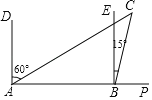
【题目】如图,一游船往返于A,B,C三岛,此船从A岛出发向正东方向航行1小时到达B岛,C岛在A岛的北偏东60°方向,在B岛的北偏东15°方向,已知游船的航速为20海里/小时,求此船从B岛航行到C岛需要多少小时?(![]() ≈1.414,结果精确到0.1小时)
≈1.414,结果精确到0.1小时)
查看答案和解析>>
科目:初中数学 来源: 题型:
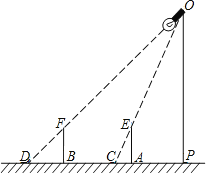
【题目】如图,学校操场旁立着一杆路灯(线段OP).小明拿着一根长2m的竹竿去测量路灯的高度,他走到路灯旁的一个地点A竖起竹竿(线段AE),这时他量了一下竹竿的影长AC正好是1m,他沿着影子的方向走了4m到达点B,又竖起竹竿(线段BF),这时竹竿的影长BD正好是2m,请利用上述条件求出路灯的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com