
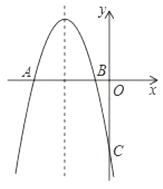
【题目】如图所示,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,![]() ,与
,与![]() 轴交于
轴交于![]() ,并且对称轴
,并且对称轴![]() .
.

(1)求抛物线的解析式;
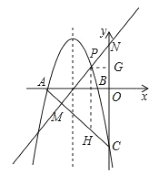
(2)![]() 在
在![]() 轴上方的抛物线上,过
轴上方的抛物线上,过![]() 的直线
的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)点![]() 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当![]() 是以
是以![]() 为直角边的直角三角形时,求
为直角边的直角三角形时,求![]() 点坐标;
点坐标;
【答案】(1)![]() ;(2)
;(2)![]() 的最大值为
的最大值为![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)利用待定系数法求解可得;
(2)先求AC解析式,作PH∥y轴交AC于H,作PG⊥y轴,设出P的坐标,,由MN的解析式的特点判断![]() ,利用三角函数把PM,PN的长度转化到PH,PG的上,利用
,利用三角函数把PM,PN的长度转化到PH,PG的上,利用![]() 及二次函数的性质进一步求解可得;
及二次函数的性质进一步求解可得;
(3)设D(-3,y),利用两点间的距离公式得到![]() ,然后分类:当△ACD是以AC为直角边、CD为斜边和以AC为直角边、AD为斜边的直角三角形时,分别解方程求出y即可得到对应的D点坐标;
,然后分类:当△ACD是以AC为直角边、CD为斜边和以AC为直角边、AD为斜边的直角三角形时,分别解方程求出y即可得到对应的D点坐标;
解:(1)∵抛物线过![]() ,对称轴为直线
,对称轴为直线![]() ,∴点
,∴点![]() 坐标为
坐标为![]() ,
,
可设抛物线解析式为![]() ,将点
,将点![]() 代入,得:
代入,得:![]() ,
,
解得![]() ,则抛物线解析式为
,则抛物线解析式为![]() ;
;
(2)设![]() 点坐标为
点坐标为![]() ,
,
∴直线![]() 解析式为
解析式为![]() ,
,
过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,作
,作![]() 轴于
轴于![]() ,
,
![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() 的最大值为
的最大值为![]() ;
;
(3)①设![]() ,
,
则![]() ,
,
当![]() 是以
是以![]() 为直角边、
为直角边、![]() 为斜边的直角三角形时,
为斜边的直角三角形时,
![]() ,即
,即![]() ,
,
解得![]() ,此时
,此时![]() ;
;
当![]() 是以
是以![]() 为直角边、
为直角边、![]() 为斜边的直角三角形时,
为斜边的直角三角形时,
![]() ,即
,即![]() ,
,
解得![]() ,此时点
,此时点![]() ;
;
综上,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(不与端点重合),
上(不与端点重合),![]() ,射线
,射线![]() 交
交![]() 延长线于点
延长线于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() .
.
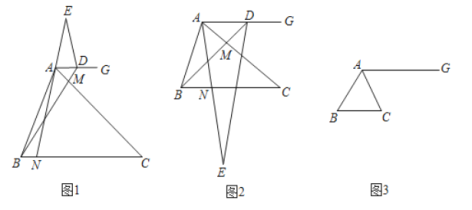
(1)(观察猜想)如图1,点![]() 在射线
在射线![]() 上,当
上,当![]() 时,
时,
①线段![]() 与
与![]() 的数量关系是______;
的数量关系是______;
②![]() 的度数是______;
的度数是______;
(2)(探究证明)如图2点![]() 在射线
在射线![]() 上,当
上,当![]() 时,判断并证明线段
时,判断并证明线段![]() 与
与![]() 的数量关系,求
的数量关系,求![]() 的度数;
的度数;
(3)(拓展延伸)如图3,点![]() 在直线
在直线![]() 上,当
上,当![]() 时,
时,![]() ,点
,点![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年2月18日,《感动中国2018年度人物颁奖盛典》在央视综合频道播出,其中乡村教师张玉滚的事迹令人非常感动某校团委组织“支援乡村教育,帮助教师张玉滚”的捐款活动,以下为九年级(1)班捐款情况:
捐款金额(元) | 5 | 10 | 20 | 50 |
人数(人) | 12 | 13 | 16 | 11 |
则这个班学生捐款金额的中位数和众数分别为( )
A.15,50B.20,20C.10,20D.20,50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
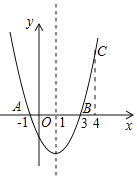
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的是_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
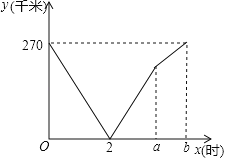
【题目】已知![]() 、
、![]() 两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从
两地之间有一条270千米的公路,甲、乙两车同时出发,甲车以60千米/时的速度沿此公路从![]() 地匀速开往
地匀速开往![]() 地,乙车从
地,乙车从![]() 地沿此公路匀速开往
地沿此公路匀速开往![]() 地,两车分别到达目的地后停止.甲、乙两车相距的路程
地,两车分别到达目的地后停止.甲、乙两车相距的路程![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (时)之间的函数关系如图所示.
(时)之间的函数关系如图所示.
(1)乙车的速度为 千米/时,![]() ,
,![]() .
.
(2)求甲、乙两车相遇后![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)当甲车到达距![]() 地70千米处时,求甲、乙两车之间的路程.
地70千米处时,求甲、乙两车之间的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
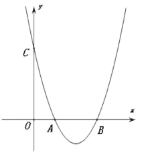
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(3)在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com