
【题目】已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(不与端点重合),
上(不与端点重合),![]() ,射线
,射线![]() 交
交![]() 延长线于点
延长线于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() .
.
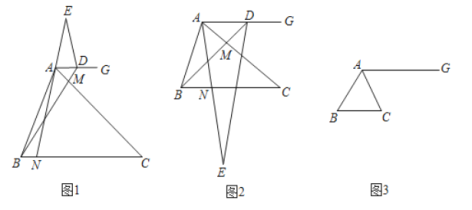
(1)(观察猜想)如图1,点![]() 在射线
在射线![]() 上,当
上,当![]() 时,
时,
①线段![]() 与
与![]() 的数量关系是______;
的数量关系是______;
②![]() 的度数是______;
的度数是______;
(2)(探究证明)如图2点![]() 在射线
在射线![]() 上,当
上,当![]() 时,判断并证明线段
时,判断并证明线段![]() 与
与![]() 的数量关系,求
的数量关系,求![]() 的度数;
的度数;
(3)(拓展延伸)如图3,点![]() 在直线
在直线![]() 上,当
上,当![]() 时,
时,![]() ,点
,点![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() ;(3)满足条件的
;(3)满足条件的![]() 的长为
的长为![]() 或4.
或4.
【解析】
(1)①延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点O,先由等边对等角得到
于点O,先由等边对等角得到![]() ,然后证明
,然后证明![]() ,即可得到BM=AN;②再由等边对等角和平行线推出
,即可得到BM=AN;②再由等边对等角和平行线推出![]() ,由三角形外角性质得到
,由三角形外角性质得到![]() ,可推出
,可推出![]() ,即可得
,即可得![]() .
.
(2)同理可证![]() ,同(1)可推出
,同(1)可推出 ![]() ,最后得到
,最后得到![]() .
.
(3)当![]() 时,作
时,作![]() 于
于![]() ,在
,在![]() 中,利用60°可求出边长,然后在在
中,利用60°可求出边长,然后在在![]() 中求出BM,再由
中求出BM,再由![]() ,利用相似比求出CF,当
,利用相似比求出CF,当![]() 时,同法可求
时,同法可求![]() .
.
(1)①如图1中,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点O.
于点O.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
②∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵∠ANB+∠ENF=180°,∠BMA+∠BMC=180°,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为①![]() ,②
,②![]() .
.
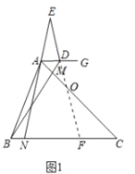
(2)如图2中,设![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

(3)①如图3-1中,当![]() 时,作
时,作![]() 于
于![]() .
.
由题意![]() ,在
,在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,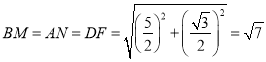 ,
,
由(2)可知:![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
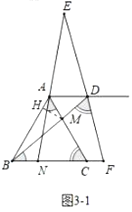
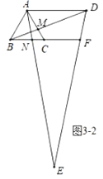
②如图3-2中,当![]() 时,同法可得
时,同法可得![]() .
.
综上所述,满足条件的![]() 的长为
的长为![]() 或4.
或4.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
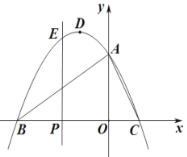
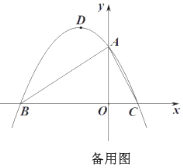
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点
两点
(点![]() 在点
在点![]() 的左侧),抛物线的顶点为
的左侧),抛物线的顶点为![]() .
.
(1)求抛物线的表达式;
(2)用配方法求点![]() 的坐标;
的坐标;
(3)点![]() 是线段
是线段![]() 上的动点.
上的动点.
①过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
②在①的条件下,点![]() 是坐标轴上的点,且点
是坐标轴上的点,且点![]() 到
到![]() 和
和![]() 的距离相等,请直接写出线段
的距离相等,请直接写出线段![]() 的长;
的长;
③若点![]() 是射线
是射线![]() 上的动点,且始终满足
上的动点,且始终满足![]() ,连接
,连接![]() ,
,![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,E为BC的中点,过点E作EF⊥AB于点F,延长DC,交FE的延长线于点G,连结DF,已知∠FDG=45°
(1)求证:GD=GF.
(2)已知BC=10, ![]() .求 CD的长.
.求 CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
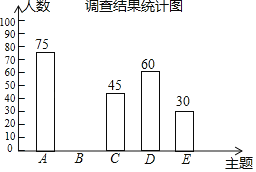
【题目】2019年3月19日,河南省教育厅发布《关于推进中小学生研学旅行的实施方案》,某中学为落实方案,给学生提供了以下五种主题式研学线路:A.“红色河南”,B.“厚重河南”C.“出彩河南”,D.“生态河南”,E.“老家河南”为了解学生最喜欢哪一种研学线路(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:
调查结果统计表
主题 | 人数/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受调查的总人数为 人,统计表中m= ,n= .
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则“生态河南”主题线路所在扇形的圆心角度是 .
(4)若该实验中学共有学生3000人,请据此估计该校最喜欢“老家河南”主题线路的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 的图象经过
的图象经过![]() 和
和![]() 两点,且与
两点,且与![]() 轴交于
轴交于![]() ,直线
,直线![]() 是抛物线的对称轴,过点
是抛物线的对称轴,过点![]() 的直线
的直线![]() 与直线相交于点
与直线相交于点![]() ,且点
,且点![]() 在第一象限.
在第一象限.

(1)求该抛物线的解析式;
(2)若直线![]() 和直线
和直线![]() 、
、![]() 轴围成的三角形面积为6,求此直线的解析式;
轴围成的三角形面积为6,求此直线的解析式;
(3)点![]() 在抛物线的对称轴上,
在抛物线的对称轴上,![]() 与直线
与直线![]() 和
和![]() 轴都相切,求点
轴都相切,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测量操控者A和教学楼BC距离为57米,求教学楼BC的高度.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
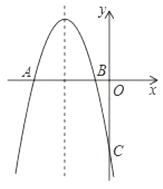
【题目】如图所示,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,![]() ,与
,与![]() 轴交于
轴交于![]() ,并且对称轴
,并且对称轴![]() .
.

(1)求抛物线的解析式;
(2)![]() 在
在![]() 轴上方的抛物线上,过
轴上方的抛物线上,过![]() 的直线
的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)点![]() 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当![]() 是以
是以![]() 为直角边的直角三角形时,求
为直角边的直角三角形时,求![]() 点坐标;
点坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com