
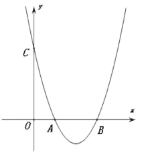
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)利用直尺和圆规,作出抛物线y=x2+mx+n的对称轴(尺规作图,保留作图痕迹,不写作法);
(2)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;
(3)在(2)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为 .
【答案】(1)作图见解析;(2)y=x2﹣4x+3;(3)3![]() .
.
【解析】
(1)利用基本作图,作AB的垂直平分线即可;
(2)根据等腰直角三角形的性质得到OB=OC=3,则C(0,3),B(3,0),然后利用待定系数法求抛物线解析式;
(3)连接BC交直线l于P,如图,根据两点之间线段最短可判断此时PC+PA的值最小,然后根据等腰直角三角形的性质计算出BC即可.
(1)如图,直线l为所作;
(2)∵△OBC是等腰直角三角形,且其腰长为3,即OB=OC=3,∴C(0,3),B(3,0),把C(0,3),B(3,0)分别代入y=x2+mx+n得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为y=x2﹣4x+3;
,∴抛物线解析式为y=x2﹣4x+3;
(3)连接BC交直线l于P,如图,则PA=PB.
∵PC+PA=PC+PB=BC,∴此时PC+PA的值最小,而BC=![]() OB=3
OB=3![]() ,∴PA+PC的最小值为3
,∴PA+PC的最小值为3![]() .
.
故答案为:3![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
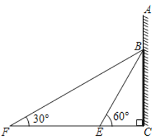
【题目】如图,在某建筑物AC上,挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行30米到达点E处,看到条幅顶端B,测得仰角为60°,求宣传条幅BC的长.(注:不计小明的身高,结果精确到1米,参考数据![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,![]() ,与
,与![]() 轴交于
轴交于![]() ,并且对称轴
,并且对称轴![]() .
.
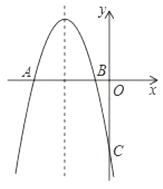

(1)求抛物线的解析式;
(2)![]() 在
在![]() 轴上方的抛物线上,过
轴上方的抛物线上,过![]() 的直线
的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)点![]() 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当![]() 是以
是以![]() 为直角边的直角三角形时,求
为直角边的直角三角形时,求![]() 点坐标;
点坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … | - | 0 |
| 1 |
| 2 |
| … |
y | … |
| -1 | - | m | - | -1 | n | … |
则对于该函数的性质的判断:
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;
③方程ax2+bx+c=0的两个实数根分别位于-![]() <x<0和2<x<
<x<0和2<x<![]() 之间;
之间;
④当x>0时,函数值y随x的增大而增大;
其中正确的是:
A.②③B.②④C.①③D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长是4cm,点P从点A出发,沿A→B的路径运动,到B点停止运动,运动速度是1cm/s,以PD为边,在直线PD下方做正方形DPEF,连接BE,下列函数图象中能反映BE的长度y(cm)与运动时间t(s)的函数关系的是( )
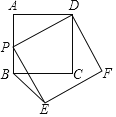
A.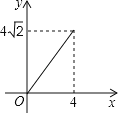 B.
B.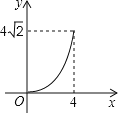
C.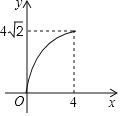 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一游船往返于A,B,C三岛,此船从A岛出发向正东方向航行1小时到达B岛,C岛在A岛的北偏东60°方向,在B岛的北偏东15°方向,已知游船的航速为20海里/小时,求此船从B岛航行到C岛需要多少小时?(![]() ≈1.414,结果精确到0.1小时)
≈1.414,结果精确到0.1小时)
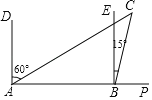
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有下列说法:①若
有下列说法:①若![]() ,则
,则![]() ;②若方程两根为-1和2,则
;②若方程两根为-1和2,则![]() ;③若方程
;③若方程![]() 有两个不相等的实根,则方程
有两个不相等的实根,则方程![]() 必有两个不相等的实根;④若
必有两个不相等的实根;④若![]() ,则方程有两个不相等的实根,其中结论正确的是有( )个。
,则方程有两个不相等的实根,其中结论正确的是有( )个。
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形△ABC,点 D,E 分别在 CA,CB 的延长线上,且 BE=CD,O为 BC 的中点,MO⊥AB 交 DE 于点 M,OM=![]() ,AD=2,则 AB=________________.
,AD=2,则 AB=________________.
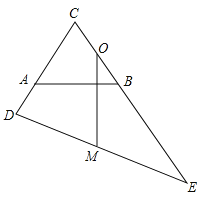
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com