
【题目】如图,矩形 ABCD 中,AB=8,BC=6,将矩形 ABCD 绕点 A 逆时针旋转得到矩形 AEFG,AE,FG 分别交射线CD 于点 PH,连结 AH,若 P 是 CH 的中点,则△APH 的周长为( )
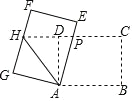
A. 15 B. 18 C. 20 D. 24
【答案】C
【解析】
连结AC,先由△AGH≌△ADH得到∠GHA=∠AHD,进而得到∠AHD=∠HAP,所以△AHP是等腰三角形,所以PH=PA=PC,所以∠HAC是直角,再在Rt△ABC中由勾股定理求出AC的长,然后由△HAC∽△ADC,根据![]() =
=![]() 求出AH的长,再根据△HAC∽△HDA求出DH的长,进而求得HP和AP的长,最后得到△APH的周长.
求出AH的长,再根据△HAC∽△HDA求出DH的长,进而求得HP和AP的长,最后得到△APH的周长.
∵P是CH的中点,PH=PC,∵AH=AH,AG=AD,且AGH与ADH都是直角,∴△AGH≌△ADH,∴∠GHA=∠AHD,又∵GHA=HAP,∴∠AHD=∠HAP,∴△AHP是等腰三角形,∴PH=PA=PC,∴∠HAC是直角,在Rt△ABC中,AC=![]() =10,∵△HAC∽△ADC,∴
=10,∵△HAC∽△ADC,∴![]() =
=![]() ,∴AH=
,∴AH=![]() =
=![]() =7.5,又∵△HAC∽△HAD,
=7.5,又∵△HAC∽△HAD,![]() =
=![]() ,∴DH=4.5,∴HP=
,∴DH=4.5,∴HP=![]() =6.25,AP=HP=6.25,∴△APH的周长=AP+PH+AH=6.25+6.25+7.5=20.
=6.25,AP=HP=6.25,∴△APH的周长=AP+PH+AH=6.25+6.25+7.5=20.


科目:初中数学 来源: 题型:
【题目】2018年12月5日,备受关注的郑州奥体中心“一场两馆”主体结构已完成,装饰装修完成![]() ,据了解,郑州奥体中心将作为2019年在郑州市举办的第十一届全国少数民族传统体自运动会主办场地,包括“一场两馆”,即
,据了解,郑州奥体中心将作为2019年在郑州市举办的第十一届全国少数民族传统体自运动会主办场地,包括“一场两馆”,即![]() 万个座位的体育场、
万个座位的体育场、![]() 万个座位的体育馆和
万个座位的体育馆和![]() 和座位的游泳馆,图1是装饰现场一辆吊车的实物图,图2是其工作示意图,
和座位的游泳馆,图1是装饰现场一辆吊车的实物图,图2是其工作示意图,![]() 是可以伸缩的起重臂,其转动点
是可以伸缩的起重臂,其转动点![]() 离地面
离地面![]() 的高度
的高度![]() 为
为![]() 当起重臂
当起重臂![]() 长度为
长度为![]() ,张角
,张角![]() 为
为![]() 时,求操作平台
时,求操作平台![]() 离地面的高度(结果保留小数点后一位参考数据:
离地面的高度(结果保留小数点后一位参考数据:![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() ;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.
;…按此规律继续旋转,直到点P2020为止,则AP2020等于_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
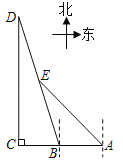
【题目】如图,为某景区五个景点A、B、C、D、E的平面示意图,B、A在C的正东方向,D在C的正北方向,D和E均在B的北偏西18°方向上,E在A的西北方向上,C、D相距1000米,E在BD的中点处,求景点B、A之间的距离.(结果保留整数)
(参考数据:sin18°≈0.3;cos18°≈0.9;tan18°≈0.3;sin72°≈0.9;cos72°≈0.3;tan72°≈3.1;![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
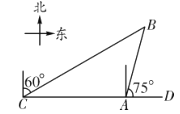
【题目】如图,港口![]() 在观测站
在观测站![]() 的正东方向
的正东方向![]() 处,某船从港口
处,某船从港口![]() 出发,沿东偏北
出发,沿东偏北![]() 方向匀速航行2小时后到达
方向匀速航行2小时后到达![]() 处,此时从观测站
处,此时从观测站![]() 处测得该船位于北偏东
处测得该船位于北偏东![]() 的方向,求该船航行的速度.
的方向,求该船航行的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
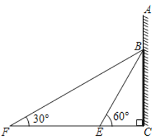
【题目】如图,在某建筑物AC上,挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行30米到达点E处,看到条幅顶端B,测得仰角为60°,求宣传条幅BC的长.(注:不计小明的身高,结果精确到1米,参考数据![]() 1.4,
1.4,![]() 1.7)
1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中.

(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标;
三个顶点的坐标;
(2)直接写出△ABC的面积为 ;
(3)在x轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … | - | 0 |
| 1 |
| 2 |
| … |
y | … |
| -1 | - | m | - | -1 | n | … |
则对于该函数的性质的判断:
①该二次函数有最大值;②不等式y>-1的解集是x<0或x>2;
③方程ax2+bx+c=0的两个实数根分别位于-![]() <x<0和2<x<
<x<0和2<x<![]() 之间;
之间;
④当x>0时,函数值y随x的增大而增大;
其中正确的是:
A.②③B.②④C.①③D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
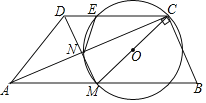
【题目】如图,在Rt△ABC中,M是斜边AB的中点,以CM为直径作圆O交AC于点N,延长MN至D,使ND=MN,连接AD、CD,CD交圆O于点E.
(1)判断四边形AMCD的形状,并说明理由;
(2)求证:ND=NE;
(3)若DE=2,EC=3,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com