【题目】如图，矩形
是由三个全等矩形拼成的，
与
，
，
，
，
分别交于点
，设
，
，
的面积依次为
，
，
，若
，则的值为（ ）
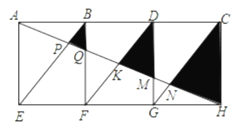
A.6B.8C.10D.12
【答案】B
【解析】
由条件可以得出△BPQ∽△DKM∽△CNH，可以求出△BPQ与△DKM的相似比为
，△BPQ与△CNH相似比为
，由相似三角形的性质，就可以求出
，从而可以求出
．
∵矩形AEHC是由三个全等矩形拼成的，
∴AB=BD=CD，AE∥BF∥DG∥CH，
∴∠BQP=∠DMK=∠CHN，
∴△ABQ∽△ADM，△ABQ∽△ACH，
∴
，
，
∵EF=FG= BD=CD，AC∥EH，
∴四边形BEFD、四边形DFGC是平行四边形，
∴BE∥DF∥CG，
∴∠BPQ=∠DKM=∠CNH，
又∵∠BQP=∠DMK=∠CHN，
∴△BPQ∽△DKM，△BPQ∽△CNH，
∴
，
，
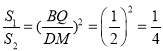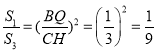即
，
，
，
∴
，即
，
解得：
，
∴
，
故选：B．
心算口算巧算一课一练系列答案
应用题作业本系列答案科目：初中数学 来源： 题型：
【题目】数学可以让人高雅，益智，豪情逸致，某中学为开拓学生视野，开展“课外学数学”活动，随机调查了九年级部分学生一周的课外学习数学时间，并将结果绘制成两幅不完整的统计图，请你根据统计图的信息回答下列问题：
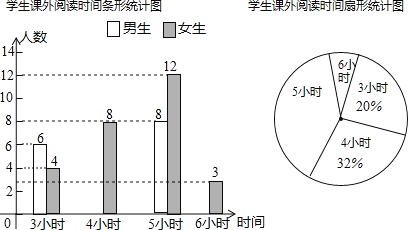
（1）本次调查的学生总数为____________人，被调查学生课外学习数学时间的中位数是____________小时，众数是 小时；
（2）请你补全条形统计图；
（3）在扇形统计图中，课外学习数学时间为5小时的扇形的圆心角度数是____________；
（4）九年级有学生700人，估计九年级一周课外学习数学时间不少于5小时小时的学生有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在正方形ABCD中，点P从点D出发，沿着D→A方向匀速运动，到达点A后停止运动，点Q从点D出发，沿着D—C—B—A的方向匀速运动，到达点A后停止运动． 已知点P的运动速度为4，图②表示P、Q两点同时出发x秒后，△APQ的面积为y与x的函数关系，则点Q的运动速度可能是（ ）
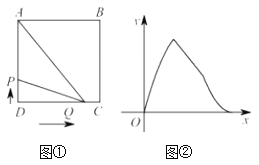
A.2B.3C.8D.12
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，抛物线y＝﹣x2+bx+c经过点A、B，C，已知A（﹣1，0），C（0，3）．
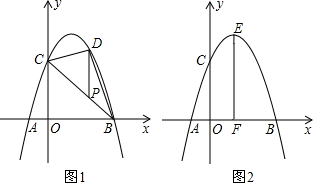
（1）求抛物线的解析式；
（2）如图1，P为线段BC上一动点，过点P作y轴的平行线，交抛物线于点D，是否存在这样的P点，使线段PD的长有最大值？若存在，求出这个最大值；若不存在，请说明理由；
（3）如图2，抛物线的顶点为E，EF⊥x轴于点F，N是直线EF上一动点，M（m，0）是x轴一个动点，请直接写出CN+MN+
MB的最小值以及此时点M、N的坐标，直接写出结果不必说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，D是△ABC的BC边上一点，连接AD，作△ABD的外接圆，将△ADC沿直线AD折叠，点C的对应点E落在⊙O上．
（1）求证：AE＝AB．
（2）填空：
①当∠CAB＝90°，cos∠ADB＝
，BE＝2时，边BC的长为 ．
②当∠BAE＝ 时，四边形AOED是菱形．
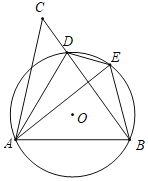
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一次函数
的图象与
轴相交于点
，与反比例函数
的图象相交于点
，
．
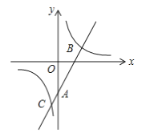
（1）求一次函数和反比例函数的解析式；
（2）根据图象，直接写出
时，
的取值范围；
（3）在轴上是否存在点
，使
为等腰三角形，如果存在，请求点的坐标，若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
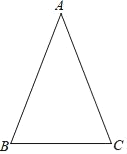
【题目】在△ABC中，AB＝AC
（1）利用直尺和圆规完成如下操作，作∠BAC的平分线和AB的垂直平分线，交点为P（不写作法，保留作图瘕迹）
（2）连结PB，若∠ABC＝65°，求∠ABP的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
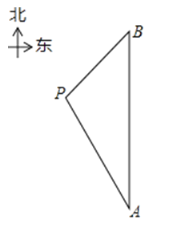
【题目】在一次海上救援中，两艘专业救助船
同时收到某事故渔船的求救讯息，已知此时救助船
在
的正北方向，事故渔船
在救助船的北偏西30°方向上，在救助船的西南方向上，且事故渔船与救助船相距120海里．
（1）求收到求救讯息时事故渔船与救助船之间的距离；
（2）若救助船A，分别以40海里/小时、30海里/小时的速度同时出发，匀速直线前往事故渔船处搜救，试通过计算判断哪艘船先到达．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
