
【题目】已知关于x的两个一元二次方程:
方程①:![]() ;
;
方程②:x2+(2k+1)x﹣2k﹣3=0.
(1)若方程①有两个相等的实数根,求:k的值
(2)若方程①和②只有一个方程有实数根,请说明此时哪个方程没有实数根.
(3)若方程①和②有一个公共根a,求代数式(a2+4a﹣2)k+3a2+5a的值.
【答案】(1)k=﹣4;(2)证明见解析;(3)5;
【解析】
(1)根据一元二次方程的定义和判别式的意义得到1+![]() ≠0且△1=0,即(k+2)2-4(1+
≠0且△1=0,即(k+2)2-4(1+![]() )×(-1)=0,求出k的值即可.(2)计算第2个方程的判别式得△2=(2k+3)2+4>0,利用判别式的意义可判断方程②总有实数根,于是可判断此时方程①没有实数根,(3)设a 是方程①和②的公共根,利用方程解的定义得到(1+
)×(-1)=0,求出k的值即可.(2)计算第2个方程的判别式得△2=(2k+3)2+4>0,利用判别式的意义可判断方程②总有实数根,于是可判断此时方程①没有实数根,(3)设a 是方程①和②的公共根,利用方程解的定义得到(1+![]() )a2+(k+2)a-1=0 ③,a2+(2k+1)a-2k-3=0④,利用③×2(2+k)a2+(2k+4)a﹣2=0⑤,由⑤+④得(3+k)a2+(4k+5)a﹣2k=5,然后利用整体代入的方法计算代数式的值.
)a2+(k+2)a-1=0 ③,a2+(2k+1)a-2k-3=0④,利用③×2(2+k)a2+(2k+4)a﹣2=0⑤,由⑤+④得(3+k)a2+(4k+5)a﹣2k=5,然后利用整体代入的方法计算代数式的值.
(1)∵方程①有两个相等的实数根,
∴![]() ,Δ1=0,
,Δ1=0,
则k≠﹣2,△1=b2﹣4ac=(k+2)2﹣4(1+![]() )×(﹣1)=k2+4k+4+4+2k=k2+6k+8,
)×(﹣1)=k2+4k+4+4+2k=k2+6k+8,
则(k+2)(k+4)=0,
∴k=﹣2,k=﹣4,
∵k≠﹣2,
∴k=﹣4;
(2)∵△2=(2k+1)2﹣4×1×(﹣2k﹣3)=4k2+4k+1+8k+12=4k2+12k+13=(2k+3)2+4>0,
∴无论k为何值时,方程②总有实数根,
∵方程①、②只有一个方程有实数根,
∴此时方程①没有实数根.
(3)根据a是方程①和②的公共根,
∴![]() ③, a2+(2k+1)a﹣2k﹣3=0④,
③, a2+(2k+1)a﹣2k﹣3=0④,
∴③×2得:(2+k)a2+(2k+4)a﹣2=0⑤,
⑤+④得:(3+k)a2+(4k+5)a﹣2k=5,
代数式=(a2+4a﹣2)k+3a2+5a=(3+k)a2+(4k+5)a﹣2k=5.
故代数式的值为5.


科目:初中数学 来源: 题型:
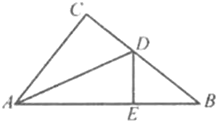
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,DE⊥AB,垂足为E,若AC=3,AB=5,则DE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
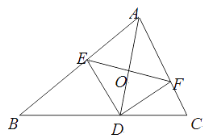
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.得到下面四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④ AE2+DF2=AF2+DE2.上述结论中正确的是( )
A. ②③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
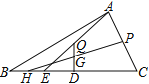
【题目】如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=![]() CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H.若BC=9,则HE=_____.
CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H.若BC=9,则HE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
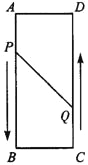
【题目】如图,已知A,B,C,D为矩形的四个顶点,AB等于16cm,AD等于6cm,动点P、Q分别从A、C同时出发,点P以3cm每秒的速度向点B移动,一直移动到点B时停止运动,当P点停止运动时Q点也停止运动,点Q以2cm每秒的速度向点D移动。
(1)P,Q两点从出发开始几秒时,四边形PBCQ的面积为33平方厘米?
(2)P,Q两点从出发开始几秒时,点P与点Q间的距离为10cm?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 和△CDE 都是等腰直角三角形,∠ACB=∠ECD=90°,D 为 AB 边上一点.如下结论:

①△ACE≌△BCD; ②△ADE 是直角三角形; ③AD2+BD2=2CD2; ④AE=AC, 其中正确的结论有( )
A.①③④B.①②③C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在由6个大小相同的小正方形组成的方格中:
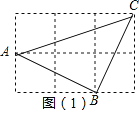
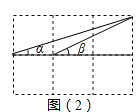
(1)如图(1),△ABC 的三个顶点A、B、C都在格点上,试判断△ABC的形状,并加以证明;
(2)如图(2),连结三格和两格的对角线,利用(1)的图形特征,求出∠α+∠β的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,△ABC为等腰直角三角形,∠ACB=90°,E是AC边上的一个动点(点E与A,C不重合),以CE为边在△ABC外作等腰直角△ECD,∠ECD=90°,连接BE,AD.猜想线段BE,AD之间的关系.
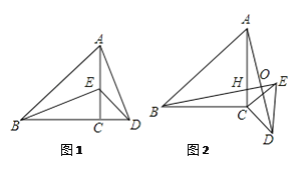
(1)独立思考:请直接写出线段BE,AD之间的数量关系:
(2)合作交流:城南中学八年级某学习小组受上述问题的启发,将图(1)中的等腰直角△ECD绕着点C顺时针方向旋转至如图(2)的位置,BE交AC于点H,交AD于点O.(1)中的结论是否仍然成立,请说明理由.
(3)拓展延伸:图(1)中AD和BE存在着怎样的位置关系?在等腰直角△ECD绕着点C顺时针方向旋转的过程中AD和BE的这种位置关系是否会变化?请结合图(2)说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为( )

A.16 B.15 C.14 D.13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com