
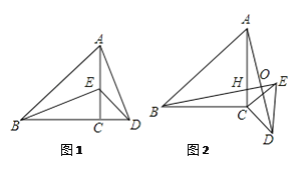
【题目】问题情境:如图1,△ABC为等腰直角三角形,∠ACB=90°,E是AC边上的一个动点(点E与A,C不重合),以CE为边在△ABC外作等腰直角△ECD,∠ECD=90°,连接BE,AD.猜想线段BE,AD之间的关系.
(1)独立思考:请直接写出线段BE,AD之间的数量关系:
(2)合作交流:城南中学八年级某学习小组受上述问题的启发,将图(1)中的等腰直角△ECD绕着点C顺时针方向旋转至如图(2)的位置,BE交AC于点H,交AD于点O.(1)中的结论是否仍然成立,请说明理由.
(3)拓展延伸:图(1)中AD和BE存在着怎样的位置关系?在等腰直角△ECD绕着点C顺时针方向旋转的过程中AD和BE的这种位置关系是否会变化?请结合图(2)说明理由.
【答案】(1)BE=AD;(2)仍成立,理由见解析;(3)成立,理由见解析
【解析】
(1)先利用边角边定理证明△BCE和△ACD全等,于是对应边BE=CD;(2)结论仍然成立,根据等腰直角三角形的性质,利用SAS定理证明△ACD≌△BCE,得对应边BE=AD;(3)因为△BCE≌△ACD,对应角∠CEB和∠CDA相等,再由同角的余角相等,可得BE⊥AD;由△BCE和△ACD全等得∠CBE=∠CAD,而∠BMC和∠AMP是对顶角,结合三角形内角和可得∠APM=90°,则BE⊥AD.
(1)解:如图(1)BE=AD,
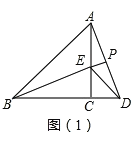
∵△ABC和△CDE都是等腰直角三角形,
∴BC=AC,CE=CD,∠BCE=∠ACD=90 ,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)不变化,理由如下:
∵△ABC和△CDE都是等腰直角三角形,
∴BC=AC,CE=DE,∠BCA=∠ECD=90°,
∴∠BCA+∠ACE=∠ECD+∠ACE,
∴∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴BE=AD,
(3)如图,
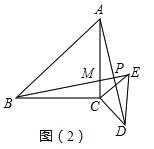
成立,理由如下:
由(1)知,△BCE≌△ACD,
∴∠CEB=∠CDA,
∵∠CBE+∠CEB=90°,
∴∠CBE+∠CDA=90°,
∴BE⊥AD,
由(2)得,∵△BCE≌△ACD,
∴∠CBE=∠CAD,
∠BMC=∠AMP,
∵∠APM=∠BCM=90°,
即BE⊥AD.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
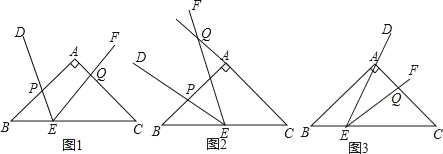
【题目】如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.
(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;
(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的两个一元二次方程:
方程①:![]() ;
;
方程②:x2+(2k+1)x﹣2k﹣3=0.
(1)若方程①有两个相等的实数根,求:k的值
(2)若方程①和②只有一个方程有实数根,请说明此时哪个方程没有实数根.
(3)若方程①和②有一个公共根a,求代数式(a2+4a﹣2)k+3a2+5a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点P是∠AOB的平分线OC上的一点,我们可以分别OA、OB在截取点M、N,使OM=ON,连结PM、PN,就可得到![]() .
.


(1)请你在图①中,根据题意,画出上面叙述的全等三角形![]() 和
和![]() ,并加以证明.
,并加以证明.
(2)请你参考(1)中的作全等三角形的方法,解答下列问题:
(Ⅰ)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系.
(Ⅱ)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(Ⅰ)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
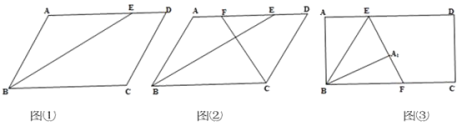
【题目】如图,城南中学八年级学习小组发现:当角平分线遇上平行线会出现等腰三角形。例如:图①,在四边形ABCD中,BE平分∠ABC,AD//BC,易得△ABE是等腰三角形。该小组将此结论作拓展:如图②,四边形ABCD中, BE平分∠BCD,CF平分∠ABC ,AD//BC,AB=CD=3,AD=4,则EF=________。如图③,如图,在长方形ABCD中,AB=3,BC=5,点E在边AD上,连接BE,△EAB沿BE翻折得到△EA1B,延长交BC于点F,若四边形EFCD的周长为11,则EF=________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班在元旦游戏活动中,有一个摸奖游戏,规则如下:不透明的盒子内有4个除颜色外完全相同的球,其中有2个红球,2个白球,摇匀后让同学们去盒子内摸球,摸到红球的就获奖,摸到白球的不获奖.
(1)现小颖有一次摸球机会,她从盒子中随机摸出1个球,求小颖获奖的概率;
(2)如果小颖、小明都有两次摸球的机会,小颖先摸出1个球,放回后再摸出1个球;小明同时摸出2个球;他们摸出的2个球中只要有红球就获奖,他们获奖的机会相等吗?请用树状图(或列表)的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
⑴若∠BAE=40°,求∠C的度数;
⑵若△ABC周长13cm,AC=6cm,求DC长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com