
【题目】如图①,点P是∠AOB的平分线OC上的一点,我们可以分别OA、OB在截取点M、N,使OM=ON,连结PM、PN,就可得到![]() .
.


(1)请你在图①中,根据题意,画出上面叙述的全等三角形![]() 和
和![]() ,并加以证明.
,并加以证明.
(2)请你参考(1)中的作全等三角形的方法,解答下列问题:
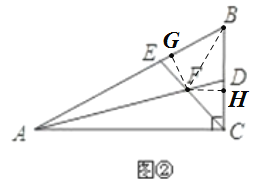
(Ⅰ)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系.
(Ⅱ)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(Ⅰ)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
【答案】(1)见详解;(2)(Ⅰ)FE=FD,证明见详解;(Ⅱ)FE=FD仍成立;理由见详解.
【解析】
(1)根据题意,画出图形,直接根据SAS,即可证明![]() ;
;
(2)(Ⅰ)过点F作FG⊥AB,FH⊥BC,垂足分别为G、H,连接BF,由角平分线性质,得到FG=FH,∠FGE=∠FHD=90°,又∠FDH=FEG=75°,由AAS证明△EFG≌△DFH,即可得到FE=FD;
(Ⅱ)与(Ⅰ)同理,得到FG=FH,∠FGE=∠FHD=90°,由∠ABC=60°,得到∠FDH=∠ABC+∠BAF=60°+∠BAF,又∠FEG =∠BAF+60°,则∠FDH=∠FEG=∠BAF+60°,然后利用AAS证明△EFG≌△DFH,即可得到结论成立.
解:(1)如图,

∵OC是∠AOB的平分线,
∴∠AOC=∠BOC,
∵OM=ON,OP=OP,
∴△POM≌△PON(SAS);
(2)(Ⅰ)如图,过点F作FG⊥AB,FH⊥BC,垂足分别为G、H,连接BF,
∵AD平分∠BAC,CE平分∠ACB,
∴点F为内心,则BF平分∠ABC,
∵FG⊥AB,FH⊥BC,
∴FG=FH,∠FGE=∠FHD=90°,
∵∠B=60°,∠ACB=90°,
∴∠BAC=30°,
∵AD平分∠BAC,CE平分∠ACB,
∴∠DAC=15°,∠ACE=45°,
∴∠FEG=∠BAC+ACE=30°+45°=75°,∠FDH=90°-15°=75°,
∴∠FDH=FEG=75°,
∴△EFG≌△DFH(AAS),
∴FE=FD;
(Ⅱ)FE=FD仍成立;理由如下:
如图,与(Ⅰ)同理,过点F作FG⊥AB,FH⊥BC,垂足分别为G、H,连接BF,

由(Ⅰ)可知,FG=FH,∠FGE=∠FHD=90°,
∵∠ABC=60°,
∴∠BAC+∠BCA=120°,
∵AD平分∠BAC,CE平分∠ACB,
∴∠FAC+∠FCA=![]() (∠BAC+∠BCA)=
(∠BAC+∠BCA)=![]() ,
,
∵∠FDH=∠ABC+∠BAF=60°+∠BAF,
∠FEG=∠BAC+∠FCA=∠BAF+∠FAC+∠FCA=∠BAF+60°,
∴∠FDH=∠FEG=∠BAF+60°,
∴△EFG≌△DFH(AAS),
∴FE=FD.


科目:初中数学 来源: 题型:
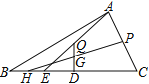
【题目】如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=![]() CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H.若BC=9,则HE=_____.
CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H.若BC=9,则HE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 和△CDE 都是等腰直角三角形,∠ACB=∠ECD=90°,D 为 AB 边上一点.如下结论:

①△ACE≌△BCD; ②△ADE 是直角三角形; ③AD2+BD2=2CD2; ④AE=AC, 其中正确的结论有( )
A.①③④B.①②③C.①②D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在由6个大小相同的小正方形组成的方格中:
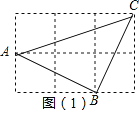
(1)如图(1),△ABC 的三个顶点A、B、C都在格点上,试判断△ABC的形状,并加以证明;
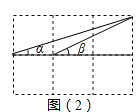
(2)如图(2),连结三格和两格的对角线,利用(1)的图形特征,求出∠α+∠β的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A.红红不是胜就是输,所以红红胜的概率为![]()
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为![]()
D.娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图1,△ABC为等腰直角三角形,∠ACB=90°,E是AC边上的一个动点(点E与A,C不重合),以CE为边在△ABC外作等腰直角△ECD,∠ECD=90°,连接BE,AD.猜想线段BE,AD之间的关系.
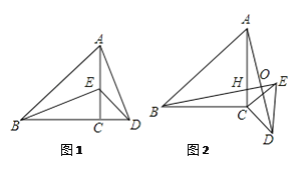
(1)独立思考:请直接写出线段BE,AD之间的数量关系:
(2)合作交流:城南中学八年级某学习小组受上述问题的启发,将图(1)中的等腰直角△ECD绕着点C顺时针方向旋转至如图(2)的位置,BE交AC于点H,交AD于点O.(1)中的结论是否仍然成立,请说明理由.
(3)拓展延伸:图(1)中AD和BE存在着怎样的位置关系?在等腰直角△ECD绕着点C顺时针方向旋转的过程中AD和BE的这种位置关系是否会变化?请结合图(2)说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
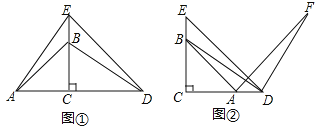
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com