
【题目】在![]() 中,
中,![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)若![]() ,则
,则![]() 为 度;
为 度;
(2)如果![]() (
(![]() ),其余条件不变,求
),其余条件不变,求![]() 的度数;
的度数;
(3)补全规律:等腰三角形一腰的垂直平分线与 相交所成的锐角等于 .
【答案】(1)20°;(2)![]()
![]() ;(3)底边所在直线,顶角的一半
;(3)底边所在直线,顶角的一半
【解析】
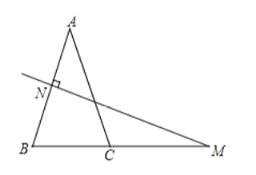
(1)根据等腰三角形性质可得∠B=70°,再根据线段垂直平分线的性质得到∠M=90°-∠B=20°;
(2)与(1)同理,可得∠M=90°-∠B=90°-![]() (180°-
(180°-![]() )=
)=![]()
![]() ;
;
(3)结合(1)(2)可得到:等腰三角形一腰的垂直平分线与底边所在直线相交所成的锐角等于顶角的一半 .
(1)∵∠A=40°,AB=AC,∴∠B=![]() (180°-∠A)=
(180°-∠A)=![]() (180°-40°)=70°,∵MN是AB的垂直平分线,∴MN⊥AB,∴∠M=90°-∠B=90°-70°=20°;
(180°-40°)=70°,∵MN是AB的垂直平分线,∴MN⊥AB,∴∠M=90°-∠B=90°-70°=20°;
(2)如果![]() (
(![]() ),
),
∵![]() ,AB=AC,∴∠B=
,AB=AC,∴∠B=![]() (180°-∠A)=
(180°-∠A)=![]() (180°-
(180°-![]() ),∵MN是AB的垂直平分线,∴MN⊥AB,∴∠M=90°-∠B=90°-
),∵MN是AB的垂直平分线,∴MN⊥AB,∴∠M=90°-∠B=90°-![]() (180°-
(180°-![]() )=
)=![]()
![]() ;
;
(3)由(1)和(2)可得规律:等腰三角形一腰的垂直平分线与底边所在直线相交所成的锐角等于顶角的一半 .


科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB:![]() 交y轴于点
交y轴于点![]() ,交x轴于点B.
,交x轴于点B.

(1)求直线AB的表达式和点B的坐标;
(2)直线l垂直平分OB交AB于点D,交x轴于点E,点P是直线l上一动点,且在点D的上方,设点P的纵坐标为n.
①当![]() 时,求点P的坐标;
时,求点P的坐标;
②在①的条件下,以PB为斜边在第一象限作等腰直角![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF. 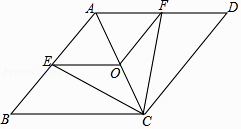
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角. 
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件工程甲独做50天可完,乙独做75天可完,现在两个人合作,但是中途乙因事离开几天,从开工后40天把这件工程做完,则乙中途离开了( )天.
A. 10 B. 20 C. 30 D. 25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣5|+(b﹣1)2=0.(友情提醒:钟表指针走动的方向为顺时针方向)
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动18秒,射线BQ才开始绕点B逆时针旋转,在射线BQ到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 内一点.
内一点.
(1)如图1,连接![]() ,将
,将![]() 沿射线
沿射线![]() 方向平移,得到
方向平移,得到![]() ,点
,点![]() 的对应点分别为点
的对应点分别为点![]() ,连接
,连接![]() .如果
.如果![]() ,
,![]() ,则
,则![]() .
.
(2)如图2,连接![]() ,当
,当![]() 时,求
时,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=![]() x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)若P是抛物线对称轴上一动点,△ACP周长最小时,求出P的坐标;
(3)是否存在抛物在线一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若不存在,请说明理由;
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问![]() 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com