
【题目】已知关于x的方程x2-3x+c=0有两个实数根.
(1)求c的取值范围;
(2)若c为正整数,取符合条件的c的一个值,并求出此时原方程的根.
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点表示的数分别为a、b,且a、b满足|a+2|+(b-8)2=0,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0)
![]()
(1) ① 线段AB的中点表示的数为___________
② 用含t的代数式表示:t秒后,点P表示的数为___________
(2) 求当t为何值时,PQ=![]() AB
AB
(3) 若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A:绿化造林. B:汽车限行.C:拆除燃煤小锅炉.D:使用清洁能源.调查过程中随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:

(1)这次被调查的市民共有多少人?
(2)请你将统计图1补充完整;
(3)求图2中D项目对应的扇形的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了多少名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数是多少?
(2)将条形统计图补充完整;
(3)该校共有900名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD为正方形,E是BC的中点,连接AE,过点A作∠AFD,使∠AFD=2∠EAB,AF交CD于点F,如图①,易证:AF=CD+CF.
(1)如图②,当四边形ABCD为矩形时,其他条件不变,线段AF,CD,CF之间有怎样的数量关系?请写出你的猜想,并给予证明;
(2)如图③,当四边形ABCD为平行四边形时,其他条件不变,线段AF,CD,CF之间又有怎样的数量关系?请直接写出你的猜想.
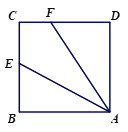
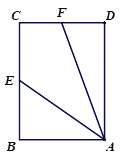
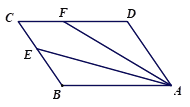
图① 图② 图③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=3x与反比例函数y=![]() (k≠0)的图象交于A(1,m)和点B.
(k≠0)的图象交于A(1,m)和点B.

(1)求m,k的值,并直接写出点B的坐标;
(2)过点P(t,0)(-1≤t≤1)作x轴的垂线分别交直线y=3x与反比函数y=![]() (k≠0)的图象于点E,F.
(k≠0)的图象于点E,F.
①当t=![]() 时,求线段EF的长;
时,求线段EF的长;
②若0<EF≤8,请根据图象直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“4000辆自行车、187个服务网点”,某市区现已实现公共自行车服务全覆盖,为人们的生活带来了方便。图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A,D,C,E在同一条直线上,CD=30 cm,DF=20 cm,AF=25 cm,FD⊥AE于点D,座杆CE=15 cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

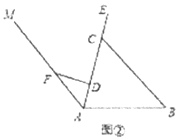
查看答案和解析>>
科目:初中数学 来源: 题型:
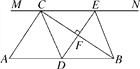
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=6,过点C的直线MN∥AB,D为AB上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE.
(1)当点D是AB的中点时,四边形BECD是什么特殊四边形?说明你的理由;
(2)在(1)的条件下,当∠A等于多少度时,四边形BECD是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个整数点![]() 即各点均表示整数
即各点均表示整数![]() ,且
,且![]() ,若A、D两点表示的数的分别为
,若A、D两点表示的数的分别为![]() 和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是
和6,点E为BD的中点,那么该数轴上上述五个点所表示的整数中,离线段BD的中点最近的整数是![]()
![]()
![]()
A. ![]() B. 0C. 1D. 2
B. 0C. 1D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com