
【题目】如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连接CG.求证:
(1)△ABM≌△CBM;
(2)CG⊥CM.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用正方形的性质得出AB=CB,∠ABM=∠CBM,进而利用SAS得出答案;
(2)直接利用全等三角形的性质得出∠BAM=∠BCM,进而得出∠BAM=∠F,∠BCM=∠GCF进而求出答案.
证明:(1)∵四边形ABCD是正方形,
∴AB=CB,∠ABM=∠CBM,
在△ABM和△CBM中,
∴△ABM≌△CBM(SAS),
(2)∵△ABM≌△CBM,
∴∠BAM=∠BCM,
∵∠ECF=90°,G是EF的中点,
∴GC=GF,
∴∠GCF=∠F,
又∵AB∥DF,
∴∠BAM=∠F,
∴∠BCM=∠GCF,
∴∠BCM+∠GCE=∠GCF+∠GCE=90°,
∴GC⊥CM.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
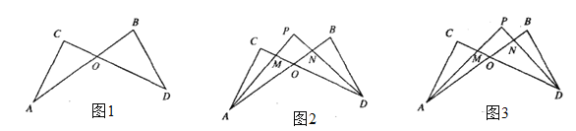
【题目】如图1,线段AB、CD相交于点O,连结AC、BD,我们把形如图1的图形称之为“8字形”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥聪明才智,解决以下问题:
(1)在图1中,请写出∠A、∠B、∠C、∠D之间的数量关系,并说明理由;
(2)仔细观察,在图2中“8字形”的个数有 个;
(3)在图2中,若∠B=70°,∠C=84°,∠CAB和∠BDC的平分线AP和DP相交于点P,并且与CD、AB分别相交于M、N利用(1)的结论,试求∠P的度数;
(4)在图3中,如果∠B和∠C为任意角,并且AP和DP分别是∠CAB和∠BDC的四等分线,即∠PAO=![]() ∠CAO, ∠BDP=
∠CAO, ∠BDP=![]() ∠BDO,那么∠P与∠C、∠B之间存在的数量关系是 (直接写出结论即可).
∠BDO,那么∠P与∠C、∠B之间存在的数量关系是 (直接写出结论即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则CF:AB的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的方格地面上,标有编号A,B,C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.
(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A地某厂和B地某厂同时制成机器若干台,A地某厂可支援外地10台,B地某厂可支援外地4台,现决定给C地8台,D地6台.已知从A运往D、C两地的运费分别是200元每台、400元每台,从B运往D、C两地的运费分别是150元每台、250元每台.
(1)设B地某厂运往D地x台,求总运费为多少元?
(2)在(1)中,当x=2时,总运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为 . 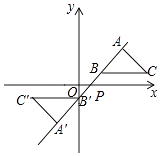
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知l1//l2,射线MN分别和直线l1,l2交于点A,B,射线ME分别和直线l1,l2交于点C,D,点P在射线MN上运动(P点与A,B,M三点不重合),设∠PDB=α ,∠PCA=β ,∠CPD=γ .
(1)如果点P在A,B两点之间运动时,α,β,γ之间有何数量关系?请说明理由;
(2)如果点P在A,B两点之外运动时,α,β,γ之间有何数量关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=![]() ∠CGE.其中正确的结论是( )
∠CGE.其中正确的结论是( )

A. ②③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com