
 如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若∠PMO=33°,∠PNO=70°,则∠QPN的度数为
如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若∠PMO=33°,∠PNO=70°,则∠QPN的度数为| 180°-66° |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
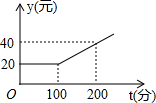 已知甲、乙两家通信公司都推出了市话通话优惠业务,甲公司每月的市话费标准如图所示,乙公司每月通话收费标准如表所示.
已知甲、乙两家通信公司都推出了市话通话优惠业务,甲公司每月的市话费标准如图所示,乙公司每月通话收费标准如表所示.| 月租费 | 通话费 |
| 25元 | 0.15元/分钟 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com