
分析 (1)先移项,再求出b2-4ac的值,最后代入公式求出即可;
(2)配方后开方,即可得出两个一元一次方程,求出方程的解即可;
(3)先配方后开方,即可得出两个一元一次方程,求出方程的解即可;
(4)整理后求出b2-4ac的值,最后代入公式求出即可.
解答 解:(1)x2+3x=1,
x2+3x-1=0,
b2-4ac=32-4×1×(-1)=13,
x=$\frac{-3±\sqrt{13}}{2}$,
x1=$\frac{-3+\sqrt{13}}{2}$,x2=$\frac{-3-\sqrt{13}}{2}$;
(2)x2-10x+25=7,
(x-5)2=7,
x-5=$±\sqrt{7}$,
x1=5+$\sqrt{7}$,x2=5-$\sqrt{7}$;
(3)x2-14x=8,
x2-14x+72=8+72,
(x-7)2=57,
x-7=$±\sqrt{57}$,
x1=7+$\sqrt{57}$,x2=7-$\sqrt{57}$;
(4)x2+2x+2=8x+4,
x2-6x-2=0,
b2-4ac=(-6)2-4×1×(-2)=44,
x=$\frac{6±\sqrt{44}}{2}$,
x1=3+$\sqrt{11}$,x2=3-$\sqrt{11}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键,难度适中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
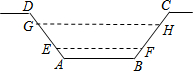 如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )
如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米.求放水后水面上升的高度是( )| A. | 0.55 | B. | 0.8 | C. | 0.6 | D. | 0.75 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
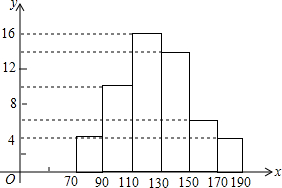 某校为预测该校九年级900名学生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分学生进行测试,并以测试数据为样本,绘制出如图所示的频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值).若次数不低于130次的成绩为优秀,估计该校成绩为优秀的人数是400.
某校为预测该校九年级900名学生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分学生进行测试,并以测试数据为样本,绘制出如图所示的频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值).若次数不低于130次的成绩为优秀,估计该校成绩为优秀的人数是400.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
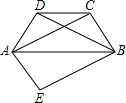 如图,在四边形ABCD中,AB∥CD,AD=BC,AC,BD是对角线且AC=BD.将△ABD沿AB对折到△ABE的位置,求证:四边形AEBC是平行四边形.
如图,在四边形ABCD中,AB∥CD,AD=BC,AC,BD是对角线且AC=BD.将△ABD沿AB对折到△ABE的位置,求证:四边形AEBC是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
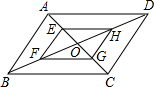 如图,在?ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别在AO,BO,CO,DO上.
如图,在?ABCD中,对角线AC与BD相交于点O,点E,F,G,H分别在AO,BO,CO,DO上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com