
【题目】![]() 年疫情期间,长沙市教育局出台《长沙市中小学线上教学工作实施意见》,长沙市推出名师公益大课堂,为学生提供线上直播教学,据统计,第一批公益课受益学生
年疫情期间,长沙市教育局出台《长沙市中小学线上教学工作实施意见》,长沙市推出名师公益大课堂,为学生提供线上直播教学,据统计,第一批公益课受益学生![]() 万人次,第三批公益课受益学生
万人次,第三批公益课受益学生![]() 万人次.
万人次.
(1)如果第二批,第三批公益课受益学生人次的增长率相同,求这个增长率;
(2)按照这个增长率,预计第四批公益课受益学生将达到多少万人次?
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已成为更多人的自主学习选择,某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论,为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
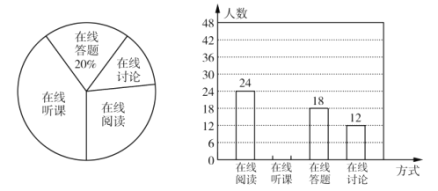
根据图中信息,解答下列问题:
(1)求本次调查的学生总人数,并通过计算补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生1800人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)试判断BC与⊙O的位置关系,并说明理由;
(2)若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的二次函数
的二次函数![]() 的图象开口向下,
的图象开口向下,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
下列判断,①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
④若![]() ,则
,则![]() ,正确的是________________(填写正确答案的序号) .
,正确的是________________(填写正确答案的序号) .
查看答案和解析>>
科目:初中数学 来源: 题型:
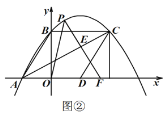
【题目】如图①,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,将
两点,将![]() 沿
沿![]() 轴正方向平移后,点
轴正方向平移后,点![]() 、点
、点![]() 的对应点分别为点
的对应点分别为点![]() 、点
、点![]() ,且四边形
,且四边形![]() 为菱形,连接
为菱形,连接![]() ,抛物线
,抛物线![]() 经过
经过![]() 三点,点
三点,点![]() 为
为![]() 上方抛物线上一动点,作
上方抛物线上一动点,作![]() ,垂足为
,垂足为![]()
![]() 求此抛物线的函数关系式;
求此抛物线的函数关系式;
![]() 求线段
求线段![]() 长度的最大值;
长度的最大值;
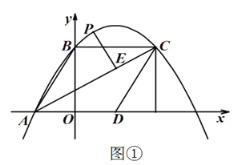
![]() 如图②,延长
如图②,延长![]() 交
交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,若
,若![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
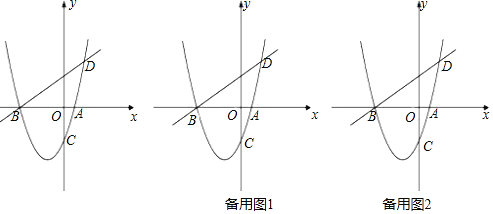
【题目】如图,已知抛物线![]() 与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且
与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C,求![]() 面积的最大值;
面积的最大值;
(3)在(2)中![]() 面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C,D为圆上的两点,OC∥BD,弦AD,BC相交于点E.
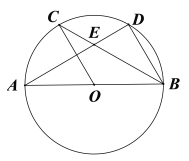
(1)求证:![]() ;
;
(2)若CE=1,EB=3,求⊙O的半径;
(3)在(2)的条件下,过点C作⊙O的切线,交BA的延长线于点P,过点P作PQ∥CB交⊙O于F,Q两点(点F在线段PQ上),求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一天,水果经营户老张用1600元从水果批发市场批发猕猴桃和芒果共50千克,后再到水果市场去卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
品名 | 猕猴桃 | 芒果 |
批发价 | 20 | 40 |
零售价 | 26 | 50 |
![]() 他购进的猕猴桃和芒果各多少千克?
他购进的猕猴桃和芒果各多少千克?
![]() 如果猕猴桃和芒果全部卖完,他能赚多少钱?
如果猕猴桃和芒果全部卖完,他能赚多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com