
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在![]() 中和
中和![]() 中,
中,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .求证:
.求证:![]() .
.
小明经探究发现,过![]() 点作
点作![]() ,交
,交![]() 于点
于点![]() (如图2),从而可证
(如图2),从而可证![]() ,使问题得到解决.
,使问题得到解决.
(1)请你按照小明单独探究思路,完成他的证明过程;
参考小明思考问题的方法,解决下面的问题:
(2)如图3,在![]() 与
与![]() 中,
中,![]() 分别为
分别为![]() 、
、![]() 的中线,连接
的中线,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,是否存在与
,是否存在与![]() 相等的线段?若存在,请找出并证明;若不存在,说明理由.
相等的线段?若存在,请找出并证明;若不存在,说明理由.

科目:初中数学 来源: 题型:
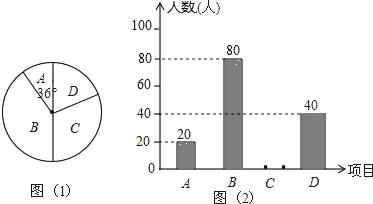
【题目】某学校为了提高学生学科能力,决定开设以下校本课程:A.文学院,B.小小数学家,C.小小外交家,D.未来科学家,为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的小小外交家的课堂学习中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加全国英语口语大赛,求恰好同时选中甲、乙两位同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
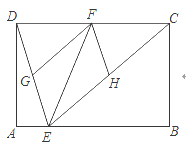
【题目】如图,已知矩形ABCD中,点E是AB边上的一个动点,点F、G、H分别是CD、DE、CE的中点.
(1)求证:四边形EHFG是平行四边形;
(2)设AB=4,AD=3,求△EFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
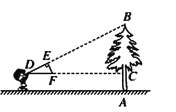
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周计划每日生产250辆摩托车,由于工人实行轮休,每日上班人数不一一定相等,实际每日的生产量与计划生产量相比情况如下表(增加的辆数为正,减少的辆数为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -4 | +27 | -23 | +14 | +1 | -18 | -15 |
根据记录回答:
(1) 本周总产量与计划量相比是增加了还是减少了?增加了或减少了多少辆?
(2)本周共生产了多少辆摩托车?
查看答案和解析>>
科目:初中数学 来源: 题型:
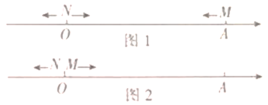
【题目】数轴上点A表示的数为10,点M,N分别以每秒a个单位长度,每秒b个单位长度的速度沿数轴运动,a, b满足|a-5|+(b-6)2=0.
(1)请真接与出a= , b= ;
(2)如图1,点M从A出发沿数轴向左运动,到达原点后立即返回向右运动:同时点N从原点0出发沿数轴向左运动,运动时间为t,点P为线段ON的中点若MP=MA,求t的值:
(3)如图2,若点M从原点向右运动,同时点N从原点向左运动,运动时间为t时M运动到点A的右侧,若此时以M,N, O, A为端点的所有线段的长度和为142,求此时点M对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个正方体的平面展开图,标注了字母M的是正方体的正面,如果正方体的左面与右面标注的式子相等.
(1)求x的值;
(2)求正方体的上面和底面的数字和.
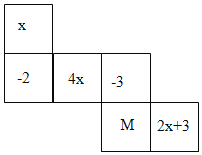
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com