
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A与原点O重合,顶点B在直线l上,将正方形沿射线OB方向无滑动地翻滚.若直线![]() ,正方形边长为2
,正方形边长为2![]()
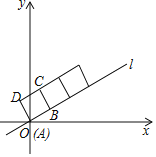
(1)翻滚后点A第一次落在直线l上的坐标是_____;
(2)当正方形翻滚2002次点A对应点的坐标是_____.
【答案】![]()
![]()
【解析】
(1)观察图形即可得到翻滚后点A第一次落在直线l上,经过四次翻滚后点A对应一个循环,解直角三角形即可求出点A第一次落在直线l上的坐标.
(2)因为点A四次翻滚为一个循环,所以求出2002除以4的余数和商即可求解.
解:(1)点B在直线![]() 上,
上,![]()
∴直线l与x轴夹角为30°,
观察图形,即可得到翻滚后点A第一次落在直线l上,
∴此时OA1=4×2![]() =8
=8![]() ,
,
∴此时A1的坐标是(![]() ×8
×8![]() ,
,![]() ×
×![]() ),
),
即(12,4![]() );
);
(2)观察图形可得经过4次翻滚后点A对应点一循环,
2002÷4=500…2,
∴经过500次翻滚后点A对应点A2000的坐标为(500×12,500×4![]() ),
),
即(6000,2000![]() ),
),
∴正方形翻滚2002次点A对应点的坐标是(6000+3×![]() ,2000
,2000![]() +3+3
+3+3![]() ),
),
即(6009﹣![]() ,
,![]() )
)
故答案为:(6009﹣![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】随着“三农”问题的解决,某农民近两年的年收入发生了明显变化,已知前年和去年的收入分别是60000元和80000元,下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图.依据统计图得出的以下四个结论正确的是( )

A. ①的收入去年和前年相同
B. ③的收入所占比例前年的比去年的大
C. 去年②的收入为2.8万
D. 前年年收入不止①②③三种农作物的收入
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AB、AC为一边,向外作正方形ABEF和正方形AGHC像这样的两个正方形称为△ABC的“依伴正方形”
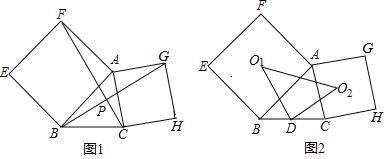
(1)如图1,连接BG,CF相交于点P,求证:BG=CF且BG⊥CF;
(2)如图2,点D是BC的中点,两个依伴正方形的中心分别为O1,O2连结O1D,O2D,O1O2:,判断△DO1O2的形状并说明由;
(3)如图2,若AB=6,AC=![]() ,∠BAC=60°,求O1O2的长.
,∠BAC=60°,求O1O2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点C是线段AB上一点,AC=![]() AB,BC为⊙O的直径.
AB,BC为⊙O的直径.
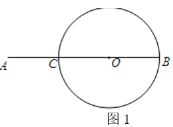
(1)在图1直径BC上方的圆弧上找一点P,使得PA=PB;(用尺规作图,保留作图痕迹,不要求写作法)
(2)连接PA,求证:PA是⊙O的切线;
(3)在(1)的条件下,连接PC、PB,∠PAB的平分线分别交PC、PB于点D、E.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O,AC为对角线,∠ACB=∠ACD
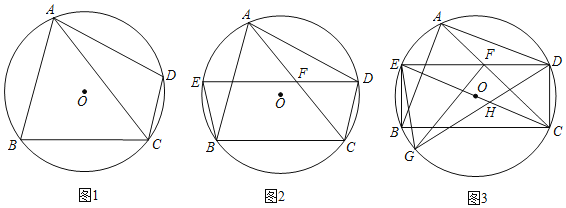
(1)如图1,求证:AB=AD;
(2)如图2,点E在AB弧上,DE交AC于点F,连接BE,BE=DF,求证:DF=DC;
(3)如图3,在(2)的条件下,点G在BC弧上,连接DG,交CE于点H,连接GE,GF,若DE=BC,EG=GH=5,S△DFG=9,求BC边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com