
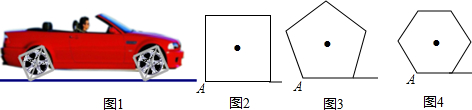
分析 (1)根据题意,画出正方形“滚动”一周后中心O所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程;
(2)根据题意,画出正五方形和正六边形“滚动”一周后中心O所经过的轨迹,然后根据弧长的计算公式求得中心O所经过的路程;
(3)根据正多边形的两顶点最长即为最大幅度计算即可.
解答 解:问题1:画出A点与O点运动的轨迹,如图所示,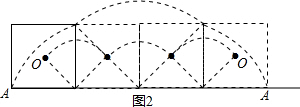
∵轮子的边长为20cm,
∴点A随该轮子滚动一周时所经过的路径长为2×$\frac{90π×20}{180}$+$\frac{90π×20\sqrt{2}}{180}$=(20π+10$\sqrt{2}$π)cm;
点O随该轮子滚动一周时所经过的路径长为3×$\frac{90π×10\sqrt{2}}{180}$=15$\sqrt{2}$π(cm);
问题2:若轮子是正五边形时,在图3中画出中心O随该轮子滚动一周时的运动路径,如图所示: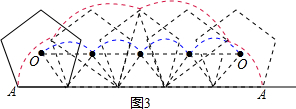
若轮子是正六边形时,在图3中画出中心O随该轮子滚动一周时的运动路径,如图所示: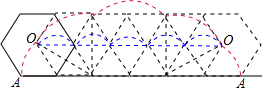
问题3: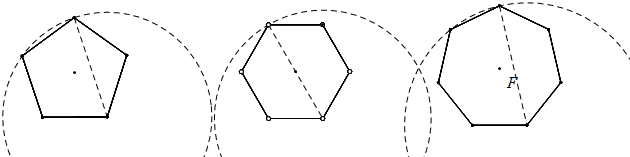
正多边形的两顶点最长即为最大幅度,可得$cosα=\frac{\frac{1}{2}×20}{\frac{1}{2}×1.7×100}$,
解得:α=83°,
所以可得内角为166°,
故边数为:360°÷(180°-166°)≈26.
故答案为:26.
点评 本题考查了弧长的计算、正方形的性质.在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=n°πR÷180°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
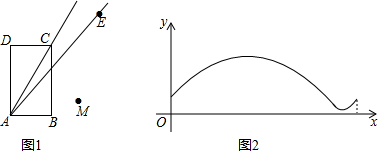
| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
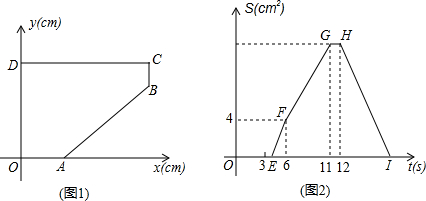
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设G是△ABC的重心,M是边AC的中点,且AC=2$\sqrt{3}$GM,D是GA延长线上任一点,连接DM,并在DM上取一点E,使∠AED=∠CAG,作CF∥AB与直线BE交于点F,CD与MF交于点H,求证:
设G是△ABC的重心,M是边AC的中点,且AC=2$\sqrt{3}$GM,D是GA延长线上任一点,连接DM,并在DM上取一点E,使∠AED=∠CAG,作CF∥AB与直线BE交于点F,CD与MF交于点H,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $x<\frac{2}{3}$ | B. | $x<\frac{3}{2}$ | C. | $x≥\frac{2}{3}$ | D. | $x≥\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com