
【题目】已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若 ![]() =
= ![]() ,如图1,.
,如图1,.
(1)判断△ABC的形状,并证明你的结论;
(2)设AE与DF相交于点M,如图2,AF=2FC=4,求AM的长.
【答案】
(1)
解:△ABC为等腰三角形,
∵△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,
∴∠CFO=∠CEO=∠BDO=∠BEO=90°,
∵四边形内角和为360°,
∴∠EOF+∠C=180°,∠DOE+∠B=180°,
∵ ![]() =
= ![]() ,
,
∴∠EOF=∠DOE,
∴∠B=∠C,AB=AC,
∴△ABC为等腰三角形;
(2)
解:连接OB、OC、OD、OF,如图,
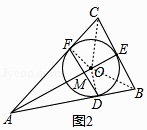
∵等腰三角形ABC中,AE⊥BC,
∴E是BC中点,BE=CE,
∵在Rt△AOF和Rt△AOD中, ![]() ,
,
∴Rt△AOF≌Rt△AOD,
∴AF=AD,
同理Rt△COF≌Rt△COE,CF=CE=2,
Rt△BOD≌Rt△BOE,BD=BE,
∴AD=AF,BD=CF,
∴DF∥BC,
∴ ![]() =
= ![]() =
=![]() ,
,
∵AE= ![]() =4
=4 ![]() ,
,
∴AM=4 ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)易证∠EOF+∠C=180°,∠DOE+∠B=180°和∠EOF=∠DOE,∠B=∠C,AB=AC,即可解题.
(2)连接OB、OC、OD、OF,易证AD=AF,BD=CF可得DF∥BC,根据平行线所截线段成比例;再根据AE长度即可解题.
【考点精析】根据题目的已知条件,利用勾股定理的概念和三角形的内切圆与内心的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() (k为常数).
(k为常数).
(1)若点P1( ![]() ,y1)和点P2(﹣
,y1)和点P2(﹣ ![]() ,y2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y1和y2的大小;
,y2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y1和y2的大小;
(2)设点P(m,n)(m>0)是其图象上的一点,过点P作PM⊥x轴于点M.若tan∠POM=2,PO= ![]() (O为坐标原点),求k的值,并直接写出不等式kx+
(O为坐标原点),求k的值,并直接写出不等式kx+ ![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
A.![]()
B.![]()
C.![]()
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF; 
(2)如图2,将 (1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论. 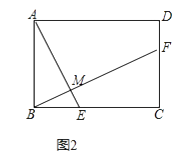
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC. 
(1)求∠CDB的度数;
(2)求证:△DCA∽△DAB;
(3)若CD的长为1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=15,AC=20,点D在边AC上,AD=5,DE⊥BC于点E,连结AE,则△ABE的面积等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.若一组数据是1,2,3,4,5,则它的方差是3
B.若分式方程 ![]() 有增根,则它的增根是1
有增根,则它的增根是1
C.对角线互相垂直的四边形,顺次连接它的四边中点所得四边形是矩形
D.若一个角的两边分别与另一个角的两边平行,则这两个角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系. 
(1)当k=4时,求这条抛物线的解析式;
(2)当k=4时,求运动员落水点与点C的距离;
(3)图中CE= ![]() 米,CF=
米,CF= ![]() 米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,东营市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题: 
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数;
(4)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com