
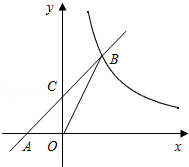
已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB=4.
(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
考点: 反比例函数综合题.
专题: 计算题;待定系数法.
分析: (1)先由A(﹣2,0),得OA=2,点B(2,n),S△AOB=4,得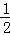 OA•n=4,n=4,则点B的坐标是(2,4),把点B(2,4)代入反比例函数的解析式为y=
OA•n=4,n=4,则点B的坐标是(2,4),把点B(2,4)代入反比例函数的解析式为y= ,可得反比例函数的解析式为:y=
,可得反比例函数的解析式为:y=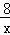 ;再把A(﹣2,0)、B(2,4)代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2.
;再把A(﹣2,0)、B(2,4)代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2.
(2)把x=0代入直线AB的解析式y=x+2得y=2,即OC=2,可得S△OCB=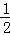 OC×2=
OC×2=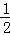 ×2×2=2.
×2×2=2.
解答: 解:(1)由A(﹣2,0),得OA=2;
∵点B(2,n)在第一象限内,S△AOB=4,
∴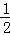 OA•n=4;
OA•n=4;
∴n=4;
∴点B的坐标是(2,4);
设该反比例函数的解析式为y=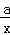 (a≠0),
(a≠0),
将点B的坐标代入,得4=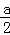 ,
,
∴a=8;
∴反比例函数的解析式为:y=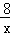 ;
;
设直线AB的解析式为y=kx+b(k≠0),
将点A,B的坐标分别代入,得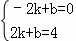 ,
,
解得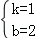 ;
;
∴直线AB的解析式为y=x+2;
(2)在y=x+2中,令x=0,得y=2.
∴点C的坐标是(0,2),
∴OC=2;
∴S△OCB= OC×2=
OC×2= ×2×2=2.
×2×2=2.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
书店卖课本和笔记本,课本每本定价20元,笔记本每本定价2元.书店开展促销活动,向客户提供两种优惠方案:①买一本课本送一本笔记本;②课本和笔记本都按定价的95%付款.现某班要到该书店购买课本50本,笔记本x本(x>50).(用含x的代数式表示(1))
(1)若该客户按方案①购买,需付款 元;
若该客户按方案②购买,需付款 元;
(2)若x=300,通过计算说明此时按哪种方案购买较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
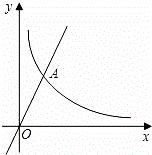
已知图中的曲线函数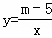 (m为常数)图象的一支.
(m为常数)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com