
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() ΝΫΒψ(Βψ
ΝΫΒψ(Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ΒΡΉσ≤ύ)Θ§”κ
ΒΡΉσ≤ύ)Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Ν§Ϋ”
Ν§Ϋ”![]() Βψ
Βψ![]() «ΒΎ“ΜœσœόΡΎ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§Βψ
«ΒΎ“ΜœσœόΡΎ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§Βψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ÷αΘ§¥ΙΉψΈΣΒψ
÷αΘ§¥ΙΉψΈΣΒψ![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() ΙΐΒψ
ΙΐΒψ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ°
Θ°
Θ®1Θ©«σ![]() »ΐΒψΒΡΉχ±ξΘΜ
»ΐΒψΒΡΉχ±ξΘΜ
Θ®2Θ© ‘ΧΫΨΩ‘ΎΒψ![]() ‘ΥΕ·Ιΐ≥Χ÷–Θ§ «Ζώ¥φ‘Ύ’β―υΒΡΒψ
‘ΥΕ·Ιΐ≥Χ÷–Θ§ «Ζώ¥φ‘Ύ’β―υΒΡΒψ![]() ΙΒΟ“‘Βψ
ΙΒΟ“‘Βψ![]() ΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ§»τ¥φ‘ΎΘ§«κ«σ≥ω¥Υ ±Βψ
ΈΣΕΞΒψΒΡ»ΐΫ«–Έ «Β»―ϋ»ΐΫ«–ΈΘ§»τ¥φ‘ΎΘ§«κ«σ≥ω¥Υ ±Βψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©m «Βψ![]() ΒΡΚαΉχ±ξΘ§«κ”ΟΚ§
ΒΡΚαΉχ±ξΘ§«κ”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈ
ΒΡ¥ζ ΐ Ϋ±μ ΨœΏΕΈ![]() ΒΡ≥ΛΘ§≤Δ«σ≥ω
ΒΡ≥ΛΘ§≤Δ«σ≥ω![]() ΈΣΚΈ÷Β ±
ΈΣΚΈ÷Β ±![]() ”–Ήν¥σ÷ΒΘ°
”–Ήν¥σ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©¥φ‘Ύ¬ζΉψΧθΦΰΒΡΒψ
ΘΜΘ®2Θ©¥φ‘Ύ¬ζΉψΧθΦΰΒΡΒψ![]() Ήχ±ξΈΣ
Ήχ±ξΈΣ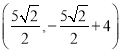 ΚΆ
ΚΆ![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©![]() ±Θ§
±Θ§![]() ”–Ήν¥σ÷ΒΘ°
”–Ήν¥σ÷ΒΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΫβΖΫ≥Χ![]() ΒΟ
ΒΟ![]() Θ§ΦΤΥψΉ‘±δΝΩΈΣ0 ±ΒΡΕΰ¥ΈΚ· ΐ÷ΒΒΟCΒψΉχ±ξΘΜ
Θ§ΦΤΥψΉ‘±δΝΩΈΣ0 ±ΒΡΕΰ¥ΈΚ· ΐ÷ΒΒΟCΒψΉχ±ξΘΜ
Θ®2Θ©άϊ”ΟΙ¥Ι…Ε®άμΦΤΥψ≥ω![]() Θ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Ω…«σΒΟ÷±œΏ
Θ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®Ω…«σΒΟ÷±œΏ![]() ΙΊœΒ ΫΈΣ
ΙΊœΒ ΫΈΣ![]() ‘ρΩ……η
‘ρΩ……η![]() ΈΣ
ΈΣ![]() Θ§
Θ§![]() Θ§Χ÷¬έΘΚΒ±
Θ§Χ÷¬έΘΚΒ±![]() ±Θ§
±Θ§![]() ΘΜΒ±
ΘΜΒ±![]() ±Θ§”–
±Θ§”–![]() ΘΜΒ±
ΘΜΒ±![]() ±Θ§”–
±Θ§”–![]() »ΜΚσΖ÷±πΫβΖΫ≥Χ«σ≥ω
»ΜΚσΖ÷±πΫβΖΫ≥Χ«σ≥ω![]() Φ¥Ω…ΒΟΒΫΕ‘”ΠΒψPΒΡΉχ±ξΘΜ
Φ¥Ω…ΒΟΒΫΕ‘”ΠΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§”…
Θ§”…![]() ÷Σ
÷Σ![]() «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Ω…≈–Εœ
«Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§Ω…≈–Εœ![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ![]() ‘Ό÷ΛΟς
‘Ό÷ΛΟς![]() ΒΟΒΫ
ΒΟΒΫ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§”Ύ «ΒΟΒΫ
Θ§”Ύ «ΒΟΒΫ![]() Θ§…η
Θ§…η![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() άϊ”Ο
άϊ”Ο![]() ΒΟΒΫ
ΒΟΒΫ![]() Θ§»ΜΚσάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΫβΨωΈ ΧβΦ¥Ω…Θ°
Θ§»ΜΚσάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ ΫβΨωΈ ΧβΦ¥Ω…Θ°
ΫβΘΚ![]() Β±
Β±![]() ±Θ§”–
±Θ§”–![]()
ΫβΒΟ![]() Θ§
Θ§
Υυ“‘![]()
Β±![]() ±Θ§”–
±Θ§”–![]()
Υυ“‘![]() Θ°
Θ°
![]() ¥φ‘ΎΘ°
¥φ‘ΎΘ°
”…Θ®1Θ©“Ή÷ΣΘ§![]() Θ§
Θ§
÷±œΏ![]() ΙΊœΒ ΫΈΣ
ΙΊœΒ ΫΈΣ![]()
…η![]() ΈΣ
ΈΣ![]() Θ§
Θ§![]() Θ§
Θ§
‘ρΔΌΒ±![]() ±Θ§
±Θ§
”–![]()
ΫβΒΟ![]() (≤ΜΚœΘ§…α»Ξ)Θ§
(≤ΜΚœΘ§…α»Ξ)Θ§
¥Υ ±![]() ΒψΈΣ
ΒψΈΣ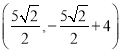
ΔΎΒ±![]() ±Θ§”–
±Θ§”–![]()
ΫβΒΟ![]() (≤ΜΚœΘ§…α»Ξ)Θ§
(≤ΜΚœΘ§…α»Ξ)Θ§
¥Υ ±![]() ΒψΈΣ
ΒψΈΣ![]()
ΔέΒ±![]() ±Θ§”–
±Θ§”–![]()
ΫβΒΟ![]() (≤ΜΚœΘ§…α»Ξ)Θ§
(≤ΜΚœΘ§…α»Ξ)Θ§
Ήέ…œΥυ ωΘ§¬ζΉψΧθΦΰΒΡΒψ![]() Ήχ±ξΈΣ
Ήχ±ξΈΣ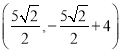 ΚΆ
ΚΆ![]() Θ°
Θ°
![]() ΙΐΒψ
ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§»γΆΦΘ§
Θ§»γΆΦΘ§
‘ρ![]() ÷αΘ§
÷αΘ§
”…![]() ÷Σ
÷Σ![]() «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
«Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
![]() Θ§
Θ§
![]() ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
ΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ
![]()
![]() Θ§
Θ§
![]()
”÷![]() Θ§
Θ§
![]()
![]()
Φ¥![]()
![]()
![]()
![]() Θ§
Θ§
…η![]() Θ§
Θ§![]() Θ§
Θ§
‘ρ![]()
![]() Θ§
Θ§
![]()
![]() Θ§
Θ§
![]() ”–Ήν¥σ÷ΒΘ§
”–Ήν¥σ÷ΒΘ§
![]() ±Θ§
±Θ§![]() ”–Ήν¥σ÷ΒΘ°
”–Ήν¥σ÷ΒΘ°


 Οϊ ΠΒΦΚΫΒΞ‘ΣΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ
Οϊ ΠΒΦΚΫΒΞ‘ΣΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ Οϊ–ΘΟϊΨμΒΞ‘ΣΆ§≤Ϋ―ΒΝΖ≤β ‘ΧβœΒΝ–¥πΑΗ
Οϊ–ΘΟϊΨμΒΞ‘ΣΆ§≤Ϋ―ΒΝΖ≤β ‘ΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
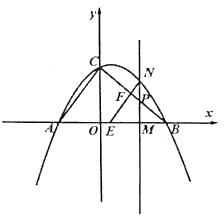
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ…œ”–«“÷Μ”–4ΗωΒψΘ§’β4ΗωΒψ÷–”–“ΜΗωΕάΧΊΒΡ–‘÷ ΘΚΝ§ΫαΟΩΝΫΒψΩ…ΒΟΒΫ6ΧθœΏΕΈΘ§’β6ΧθœΏΕΈ”–«“÷Μ”–ΝΫ÷÷≥ΛΕ»Θ°Έ“Ο«Α―’βΥΡΗωΒψ≥ΤΉςΉΦΒ»ΨύΒψΘ°άΐ»γ’ΐΖΫ–ΈABCDΒΡΥΡΗωΕΞΒψ(»γΆΦ1)Θ§”–AB=BC=CD=DAΘ§AC=BDΘ°Τδ Β¬ζΉψ’β―υ–‘÷ ΒΡΆΦ–Έ”–ΚήΕύΘ§»γΆΦ2÷–AΓΔBΓΔCΓΔOΥΡΗωΒψΘ§¬ζΉψAB=BC=CAΘ§OA=OB=OCΘΜ»γΆΦ3÷–AΓΔBΓΔCΓΔOΥΡΗωΒψΘ§¬ζΉψOA=OB=OC=BCΘ§AB=ACΘ°
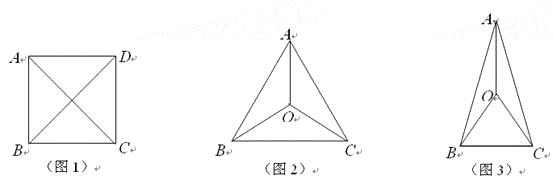
Θ®1Θ©»γΆΦΘ§»τΒ»―ϋΧί–ΈABCDΒΡΥΡΗωΕΞΒψ «ΉΦΒ»ΨύΒψΘ§«“ADΓΈBCΘ°
ΔΌ–¥≥ωœύΒ»ΒΡœΏΕΈΘ®≤Μ‘ΌΧμΦ”Ή÷ΡΗΘ©ΘΜ
ΔΎ«σΓœBCDΒΡΕ» ΐΘ°
Θ®2Θ©«κ‘ΌΜ≠≥ω“ΜΗωΥΡ±Ώ–ΈΘ§ ΙΥϋΒΡΥΡΗωΕΞΒψΈΣΉΦΒ»ΨύΒψΘ§≤Δ–¥≥ωœύΒ»ΒΡœΏΕΈΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
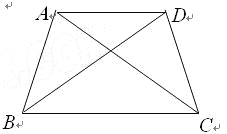
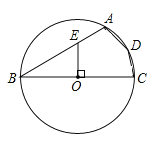
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–ΈABCD «Γ―OΒΡΡΎΫ”ΥΡ±Ώ–ΈΘ§BC «Γ―OΒΡ÷±ΨΕΘ§OEΓΆBCΫΜAB”ΎΒψEΘ§»τBE=2AEΘ§‘ρΓœADC =_________ΓψΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
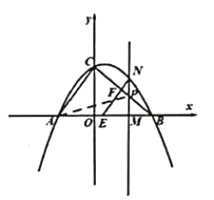
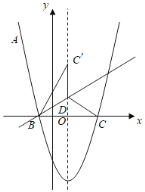
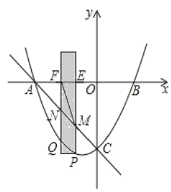
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏyΘΫ![]() ©¹2x©¹3Ψ≠ΙΐΒψAΘ®©¹2Θ§aΘ©Θ§”κx÷αœύΫΜ”ΎBΓΔCΝΫΒψΘ®BΒψ‘ΎCΒψΉσ≤ύΘ©Θ°
©¹2x©¹3Ψ≠ΙΐΒψAΘ®©¹2Θ§aΘ©Θ§”κx÷αœύΫΜ”ΎBΓΔCΝΫΒψΘ®BΒψ‘ΎCΒψΉσ≤ύΘ©Θ°
Θ®1Θ©«σaΒΡ÷ΒΦΑBΓΔCΝΫΒψΉχ±ξΘΜ
Θ®2Θ©ΒψD‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œΘ§«“ΈΜ”Ύx÷αΒΡ…œΖΫΘ§ΫΪΓςBCD―Ί÷±œΏBDΖ≠’έΒΟΒΫΓςB![]() DΘ§»τΒψ
DΘ§»τΒψ![]() «ΓΚΟ¬δ‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œΘ§«σΒψ
«ΓΚΟ¬δ‘Ύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α…œΘ§«σΒψ![]() ΚΆΒψDΒΡΉχ±ξΘΜ
ΚΆΒψDΒΡΉχ±ξΘΜ
Θ®3Θ©…ηPΘ®mΘ§-3) «ΗΟ≈ΉΈοœΏ…œ“ΜΒψΘ§ΒψQΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ§‘Ύx÷αΓΔy÷αΖ÷±π’“ΒψMΓΔNΘ§ ΙΥΡ±Ώ–ΈMNQPΒΡ÷ή≥ΛΉν–ΓΘ§«κ«σ≥ωΒψMΓΔNΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
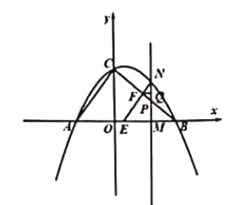
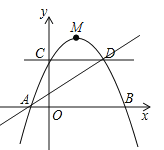
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΕΞΒψΈΣ![]() ΒΡ≈ΉΈοœΏΙΐΒψ
ΒΡ≈ΉΈοœΏΙΐΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ÷α”Ύ
÷α”Ύ![]() ΝΫΒψΘ§ΫΜ
ΝΫΒψΘ§ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() «≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ°
«≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ°
![]() «σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
![]() Β±Βψ
Β±Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΖΫ ±Θ§«σ
…œΖΫ ±Θ§«σ![]() ΟφΜΐΒΡΉν¥σ÷ΒΘ§≤Δ«σ≥ω¥Υ ±Βψ
ΟφΜΐΒΡΉν¥σ÷ΒΘ§≤Δ«σ≥ω¥Υ ±Βψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
![]() ΙΐΒψ
ΙΐΒψ![]() Ής÷±œΏ
Ής÷±œΏ![]() ΒΡ¥ΙœΏΘ§¥ΙΉψΈΣ
ΒΡ¥ΙœΏΘ§¥ΙΉψΈΣ![]() Θ§»τΫΪ
Θ§»τΫΪ![]() ―Ί
―Ί![]() Ζ≠’έΒψ
Ζ≠’έΒψ![]() ΒΡΕ‘”ΠΒψΈΣΒψ
ΒΡΕ‘”ΠΒψΈΣΒψ![]() Θ° «Ζώ¥φ‘ΎΒψ
Θ° «Ζώ¥φ‘ΎΒψ![]() Θ§ Ι
Θ§ Ι![]() «ΓΚΟ¬δ‘Ύ
«ΓΚΟ¬δ‘Ύ![]() ÷α…œΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψ
÷α…œΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψ![]() ΒΡΉχ±ξΘΚ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΒΡΉχ±ξΘΚ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
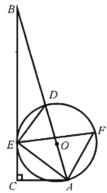
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() ΤΫΖ÷
ΤΫΖ÷![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§![]() «
«![]() …œ“ΜΒψΘ§Ψ≠Ιΐ
…œ“ΜΒψΘ§Ψ≠Ιΐ![]() Θ§
Θ§![]() ΝΫΒψΒΡ
ΝΫΒψΒΡ![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§Ής
Θ§Ής![]() ΒΡΤΫΖ÷œΏ
ΒΡΤΫΖ÷œΏ![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ°
Θ°
Θ®1Θ©«σ÷ΛΘΚ![]() «
«![]() ΒΡ«–œΏΘΜ
ΒΡ«–œΏΘΜ
Θ®2Θ©»τ![]() Θ§
Θ§![]() Θ§«σœΏΕΈ
Θ§«σœΏΕΈ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ,‘ΎΓςABC÷–,AB=ACΘ§ΒψP‘ΎBC…œΘ°
(1)«σΉς:ΓςPCD, ΙΒψD‘ΎAC…œΘ§«“ΓςPCDΓΉΓςABPΘΜ(“Σ«σ:≥ΏΙφΉςΆΦΘ§±ΘΝτΉςΆΦΚέΦΘ,≤Μ–¥ΉςΖ®)
(2)‘Ύ(1)ΒΡΧθΦΰœ¬,»τΓœAPC=2ΓœABCΘ§«σ÷Λ:PD//ABΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() .”–“ΜΩμΕ»ΈΣ1Θ§≥ΛΕ»ΉψΙΜ≥ΛΒΡΨΊ–ΈΘ®“θ”Α≤ΩΖ÷Θ©―Ί
.”–“ΜΩμΕ»ΈΣ1Θ§≥ΛΕ»ΉψΙΜ≥ΛΒΡΨΊ–ΈΘ®“θ”Α≤ΩΖ÷Θ©―Ί![]() ÷αΖΫœρΤΫ“ΤΘ§”κ
÷αΖΫœρΤΫ“ΤΘ§”κ![]() ÷αΤΫ––ΒΡ“ΜΉιΕ‘±ΏΫΜ≈ΉΈοœΏ”ΎΒψ
÷αΤΫ––ΒΡ“ΜΉιΕ‘±ΏΫΜ≈ΉΈοœΏ”ΎΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§ΫΜ÷±œΏ
Θ§ΫΜ÷±œΏ![]() ”ΎΒψ
”ΎΒψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() ΚΆΒψ
ΚΆΒψ![]() .
.
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΦΑΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®2Θ©Β±Βψ![]() ΚΆ
ΚΆ![]() ΕΦ‘ΎœΏΕΈ
ΕΦ‘ΎœΏΕΈ![]() …œ ±Θ§Ν§Ϋ”
…œ ±Θ§Ν§Ϋ”![]() Θ§»γΙϊ
Θ§»γΙϊ![]() Θ§«σΒψ
Θ§«σΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®3Θ©‘ΎΨΊ–ΈΒΡΤΫ“ΤΙΐ≥Χ÷–Θ§ «Ζώ¥φ‘Ύ“‘Βψ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ§»τ¥φ‘ΎΘ§«σ≥ωΒψ
ΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ§»τ¥φ‘ΎΘ§«σ≥ωΒψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ –Ρ≥ΧΊ≤ζΉ®¬τΒξœζ έ“Μ÷÷Οέ‘φΘ§ΟΩ«ßΩΥΒΡΫχΦέΈΣ10‘ΣΘ§œζ έΙΐ≥Χ÷–ΖΔœ÷Θ§ΟΩΧλœζΝΩ![]() ”κœζ έΒΞΦέxΘ®‘ΣΘ©÷°ΦδΙΊœΒΩ…“‘ΫϋΥΤΒΊΩ¥Ής“Μ¥ΈΚ· ΐ
”κœζ έΒΞΦέxΘ®‘ΣΘ©÷°ΦδΙΊœΒΩ…“‘ΫϋΥΤΒΊΩ¥Ής“Μ¥ΈΚ· ΐ![]() .Θ®άϊ»σ= έΦέ-ΫχΦέΘ©
.Θ®άϊ»σ= έΦέ-ΫχΦέΘ©
Θ®1Θ©–¥≥ωΟΩΧλΒΡάϊ»σwΘ®‘ΣΘ©”κœζ έΒΞΦέxΘ®‘ΣΘ©÷°ΦδΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©Β±œζ έΒΞΦέΕ®ΈΣΕύ…Ό‘Σ ±Θ§’β÷÷Οέ‘φΟΩΧλΡήΙΜΜώΒΟΉν¥σάϊ»σΘΩΉν¥σάϊ»σ «Εύ…Ό‘ΣΘΩ
Θ®3Θ©ΈοΦέ≤ΩΟ≈ΙφΕ®Θ§’β÷÷Οέ‘φΒΡœζ έΒΞΦέ≤ΜΒΟΗΏ”Ύ30‘Σ.»τ…ΧΒξœκ“Σ’β÷÷Οέ‘φΟΩΧλΜώΒΟ300‘ΣΒΡάϊ»σΘ§‘ρœζ έΒΞΦέ”ΠΕ®ΈΣΕύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com