
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .有一宽度为1,长度足够长的矩形(阴影部分)沿
.有一宽度为1,长度足够长的矩形(阴影部分)沿![]() 轴方向平移,与
轴方向平移,与![]() 轴平行的一组对边交抛物线于点
轴平行的一组对边交抛物线于点![]() 和点
和点![]() ,交直线
,交直线![]() 于点
于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() 和点
和点![]() .
.
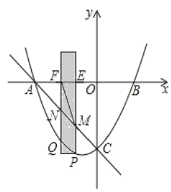
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)当点![]() 和
和![]() 都在线段
都在线段![]() 上时,连接
上时,连接![]() ,如果
,如果![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在矩形的平移过程中,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,若存在,求出点
为顶点的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() 的坐标是
的坐标是![]() ;(2)点
;(2)点![]() 坐标
坐标![]() ;(3)点
;(3)点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,点
为顶点的四边形是平行四边形时,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将点B的坐标、点C的坐标分别代入函数解析式求得b、c的值,结合抛物线解析式求得点A的坐标;
(2)作FG⊥AC于G,设点F坐标(m,0),根据sin∠AMF=![]() ,列出方程即可解决问题.
,列出方程即可解决问题.
(3))①当MN是对角线时,设点F(m,0),由QN=PM,列出方程即可解决问题.②当MN为边时,设点Q(m,![]() )则点P(m+1,
)则点P(m+1,![]() ),代入抛物线解析式,解方程即可.
),代入抛物线解析式,解方程即可.
(1)![]() 抛物线上的点
抛物线上的点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
![]() 将其代入
将其代入![]() ,得
,得![]() ,
,
解得![]() ,
,![]() .
.
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
![]() 点
点![]() 的坐标是
的坐标是![]() .
.
(2)作![]() 于
于![]() ,设点
,设点![]() 坐标
坐标![]() ,
,
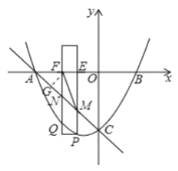
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
整理得到![]() ,
,
![]() ,
,
![]() 或
或![]() (舍弃),
(舍弃),
![]() 点
点![]() 坐标
坐标![]() .
.
(3)①当![]() 是对角线时,点
是对角线时,点![]() 在
在![]() 轴的右侧,设点
轴的右侧,设点![]() ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
![]() 点
点![]() ,点
,点![]() ,
,
![]() ,
,
![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
此时![]() ,
,
当![]() 是对角线时,点
是对角线时,点![]() 在点
在点![]() 的左侧时,设点
的左侧时,设点![]() .
.
![]() .
.
解得![]() 或
或![]() (舍弃),
(舍弃),
此时![]() ;
;
②当![]() 为边时,设点
为边时,设点![]() ,则点
,则点![]() ,
,
![]() ,
,
![]() ,
,
解得![]() .
.
![]() 点
点![]() 坐标
坐标![]() ,
,
综上所述,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,点
为顶点的四边形是平行四边形时,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() 连接
连接![]() 点
点![]() 是第一象限内抛物线上的一个动点,点
是第一象限内抛物线上的一个动点,点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() 交
交![]() 于点
于点![]() 过点
过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() .
.
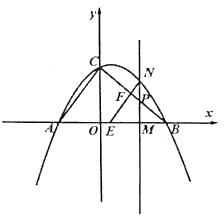
(1)求![]() 三点的坐标;
三点的坐标;
(2)试探究在点![]() 运动过程中,是否存在这样的点
运动过程中,是否存在这样的点![]() 使得以点
使得以点![]() 为顶点的三角形是等腰三角形,若存在,请求出此时点
为顶点的三角形是等腰三角形,若存在,请求出此时点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)m是点![]() 的横坐标,请用含
的横坐标,请用含![]() 的代数式表示线段
的代数式表示线段![]() 的长,并求出
的长,并求出![]() 为何值时
为何值时![]() 有最大值.
有最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() 为
为![]() 边上一点
边上一点![]() ,
,![]() .将
.将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .连接
.连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .现有以下结论:①连接
.现有以下结论:①连接![]() ,则
,则![]() 垂直平分
垂直平分![]() ;②四边形
;②四边形![]() 是菱形;③
是菱形;③![]() ;④若
;④若![]() ,则
,则![]() .其中正确的结论是________(填写所有正确结论的序号).
.其中正确的结论是________(填写所有正确结论的序号).
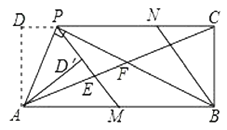
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学就“戏曲进校园”活动的喜爱情况进行了随机调查,对收集的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图所提供的信息解答下列问题:(图中![]() 表示“很喜欢”,
表示“很喜欢”,![]() 表示“喜欢”,
表示“喜欢”,![]() 表示“一般”,
表示“一般”,![]() 表示“不喜欢”)
表示“不喜欢”)
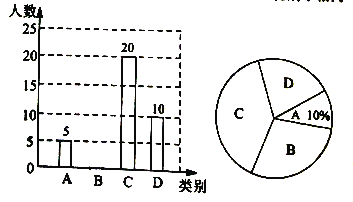
(1)被调查的总人数是_________,扇形统计图中![]() 部分所对应的扇形圆心角的度数为_________;
部分所对应的扇形圆心角的度数为_________;
(2)补全条形统计图;
(3)在抽取的![]() 类5人中,刚好有甲、乙、丙3个女生和丁、戊2个男生,从中随机抽取两个同学担任两角色,用画树状图或列表法求出抽到的两个学生性别不相同的概率.
类5人中,刚好有甲、乙、丙3个女生和丁、戊2个男生,从中随机抽取两个同学担任两角色,用画树状图或列表法求出抽到的两个学生性别不相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
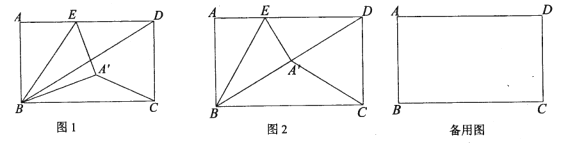
【题目】如图,在Rt△ABC中,∠C=90°,BC=2![]() ,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.
,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A. 7.5平方千米 B. 15平方千米 C. 75平方千米 D. 750平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,点E是
,点E是![]() 边上的动点,将矩形
边上的动点,将矩形![]() 沿
沿![]() 折叠,点A落在点
折叠,点A落在点![]() 处,连接
处,连接![]() .
.
(1)如图,求证:![]() ;
;
(2)如图,若点![]() 恰好落在
恰好落在![]() 上,求
上,求![]() 的值;
的值;
(3)点E在![]() 边上运动的过程中,
边上运动的过程中,![]() 的度数是否存在最大值,若存在,求出此时线段
的度数是否存在最大值,若存在,求出此时线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com