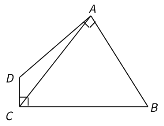
【题目】如图四边形
，
，
，
，则
的值为（ ）
A.6B.
C.
D.7
【答案】B
【解析】
过A作AE⊥AC，交CB的延长线于E，判定△ACD≌△AEB，即可得到△ACE是等腰直角三角形，DC=BE，即DC+BC=CE，根据等腰直角三角形的性质和AC的长利用勾股定理即可得出结论．
解：如图，过A作AE⊥AC，交CB的延长线于E，
∵∠DAB=∠DCB=90°，
∴∠D+∠ABC=180°=∠ABE+∠ABC，
∴∠D=∠ABE，
又∵∠DAB=∠CAE=90°，
∴∠CAD=∠EAB，
又∵AD=AB，
在△ACD和△AEB中，
，
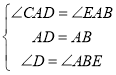∴△ACD≌△AEB（ASA），
∴AC=AE，即△ACE是等腰直角三角形，DC=BE，
∴DC+BC=CE，
∵AC=5，
∴CE=
，
故选：B．
科目：初中数学 来源： 题型：
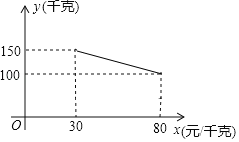
【题目】某超市销售一种商品，成本价为20元/千克，经市场调查，每天销售量y(千克)与销售单价x(元千克)之间的关系如图所示，规定每千克售价不能低于30元，且不高于80元．
(1)直接写出y与x之间的函数关系式；
(2)如果该超市销售这种商品每天获得3900元的利润，那么该商品的销售单价为多少元？
(3)设每天的总利润为w元，当销售单价定为多少元时，该超市每天的利润最大？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在矩形ABCD中，若CD＝5，以D为圆心，DC长为半径作⊙D交CA的延长线于E，过D作DF⊥AC，垂足为F，且DF＝3．
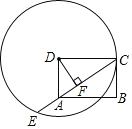
（1）求证：BC是⊙D的切线；
（2）求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】郑奶奶提着篮子去农贸市场买鸡蛋，摊主按郑奶奶的要求，用电子秤称了5千克鸡蛋，郑奶奶怀疑重量不对，把鸡蛋放入自带的质量为0.6千克的篮子中（篮子质量准确），要求放在电子秤上再称一遍，称得为5.75千克，老板客气地说：“除去篮子后为5.15千克，老顾客啦，多0.15千克就算了”，郑奶奶高兴地付了钱，满意地回家了。以下说法正确的是（ ）
A.郑奶奶赚了，鸡蛋的实际质量为5.15千克
B.郑奶奶亏了，鸡蛋的实际质量为4千克
C.郑奶奶亏了，鸡蛋的实际质量为4.85千克
D.郑奶奶不亏也不赚，鸡蛋的实际质量为5千克
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，并完成任务．
三角形的外心
定义：三角形三边的垂直平分线相交于一点，这个点叫做三角形的外心．
如图1，直线l1，l2，l3分别是边AB，BC，AC的垂直平分线．
求证：直线l1，l2，l3相交于一点．
证明：如图2，设l1，l2相交于点O，分别连接OA，OB，OC
∵l1是AB的垂直平分线，
∴OA＝OB，（依据1）
∵l2是BC的垂直平分线，
∴OB＝OC，
∴OA＝OC，（依据2）
∵l3是AC的垂直平分线，
∴点O在l3上，（依据3）
∴直线l1，l2，l3相交于一点．
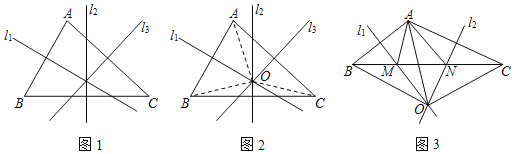
（1）上述证明过程中的“依据1”“依据2”“依据3”分别指什么？
（2）如图3，直线l1，l2分别是AB，AC的垂直平分线，直线l1，l2相交于点O，点O是△ABC的外心，l1交BC于点N，l2交BC于点N，分别连接AM、AN、OA、OB、OC．若OA＝6cm，△OBC的周长为22cm，求△AMN的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
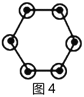
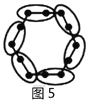
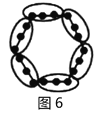
【题目】“分块计数法”：对有规律的图形进行计数时，有些题可以采用“分块计数”的方法．
例如：图1有6个点，图2有12个点，图3有18个点，…，按此规律，求图8、图
有多少个点？
我们将每个图形分成完全相同的6块，每块黑点的个数相同（如图），这样图1中黑点个数是
个；图2中黑点个数是
个；图3中黑点个数是
个；…，所以容易求出图8、图中黑点的个数分别是______、_________．
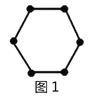
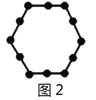
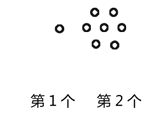
请你参考以上“分块计数法”，先将下面的点阵进行分块（画在答题卡上），再完成以下问题：
（1）第6个点阵中有______个圆圈；第个点阵中有______个圆圈．
（2）小圆圈的个数会等于331吗？请求出是第几个点阵．
查看答案和解析>>
科目：初中数学 来源： 题型：
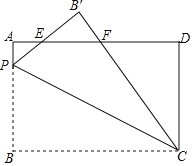
【题目】如图，矩形ABCD中，AB＝5，BC＝8，点P在AB上，AP＝1．将矩形ABCD沿CP折叠，点B落在点B'处．B'P、B′C分别与AD交于点E、F，则EF＝_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，
中，
，将扇形
按图1摆放，使扇形的半径
、
分别与
、
重合，
．
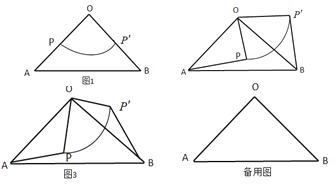
如图2，若
不动，让扇形绕点
逆时针旋转一周，连接线段
、
，设旋转角为
．
发现：直接写出、的数量关系．
探究：若
（1）扇形绕到点的左侧，当
时，旋转角
______°；
（2）扇形绕到点的右侧，当与
相切时，求；
（3）若点
是弧上任意一点，在扇形绕点逆时针转过程中，当
的面积最大时，直接写出
的度数；
延伸：如图3，若
，当
、
、
三点共线时，直接写出线段的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
，
于点
，
，为了研究图中线段之间的关系，设
，
，
（1）可通过证明
，得到
关于
的函数表达式
__________，其中自变量的取值范围是___________；
（2）根据图中给出的（1）中函数图象上的点，画出该函数的图象；
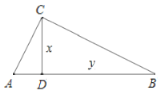
（3）借助函数图象，回答下列问题：①
的最小值是__________；②已知当
时，的形状与大小唯一确定，借助函数图象给出
的一个估计值（精确到0.1）或者借助计算给出的精确值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com