
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:填空题
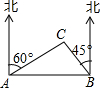 世纪中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,则建筑物C到公路AB的距离为500($\sqrt{3}$-1)m.
世纪中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50m/min的速度向正东方向行走,在A处测得建筑物C在北偏东60°方向上,20min后他走到B处,测得建筑物C在北偏西45°方向上,则建筑物C到公路AB的距离为500($\sqrt{3}$-1)m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
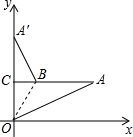 如图,Rt△AOC在平面直角坐标系中,OC在y轴上.OC=2,OA=5.将△AOC沿OB翻折使点A恰好落在y轴上的点A′的位置,则AB=$\frac{5\sqrt{21}}{7}$.
如图,Rt△AOC在平面直角坐标系中,OC在y轴上.OC=2,OA=5.将△AOC沿OB翻折使点A恰好落在y轴上的点A′的位置,则AB=$\frac{5\sqrt{21}}{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com