
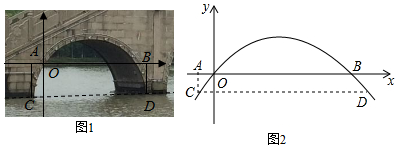
| A. | 16$\frac{9}{40}$米 | B. | $\frac{17}{4}$米 | C. | 16$\frac{7}{40}$米 | D. | $\frac{15}{4}$米 |
分析 先确定C点的横坐标,然后根据抛物线上点的坐标特征求出C点的纵坐标,从而可得到AC的长.
解答 解:∵AC⊥x轴,OA=10米,
∴点C的横坐标为-10,
当x=-10时,y=-$\frac{1}{400}$(x-80)2+16=-$\frac{1}{400}$(-10-80)2+16=-$\frac{17}{4}$,
∴C(-10,-$\frac{17}{4}$),
∴桥面离水面的高度AC为$\frac{17}{4}$m.
故选B.
点评 本题考查了二次函数的应用:利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时,要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上,从而确定抛物线的解析式,通过解析式可解决一些测量问题或其他问题.


科目:初中数学 来源: 题型:解答题
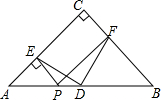 △ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.
△ABC中,∠C=90°,BC=AC,D为AB中点,P是AB上一点,PE⊥AC于E,PF⊥BC于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
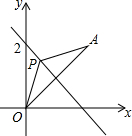 如图,平面直角坐标系中,A点坐标为(2,2),点P(m,n)在直线y=-x+2上运动,设△APO的面积为S,则下面能够反映S与m的函数关系的图象是( )
如图,平面直角坐标系中,A点坐标为(2,2),点P(m,n)在直线y=-x+2上运动,设△APO的面积为S,则下面能够反映S与m的函数关系的图象是( )| A. | 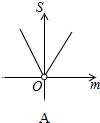 | B. | 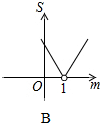 | C. | 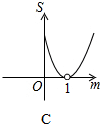 | D. | 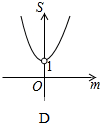 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,平面直角坐标系的原点O是正方形ABCD的中心,顶点A,B的坐标分别为(1,1),(-1,1),把正方形ABCD绕原点O逆时针旋转45°得正方形A′B′C′D′,则正方形ABCD与正方形A′B′C′D′重叠部分所形成的正八边形的边长为2$\sqrt{2}$-2.
如图,平面直角坐标系的原点O是正方形ABCD的中心,顶点A,B的坐标分别为(1,1),(-1,1),把正方形ABCD绕原点O逆时针旋转45°得正方形A′B′C′D′,则正方形ABCD与正方形A′B′C′D′重叠部分所形成的正八边形的边长为2$\sqrt{2}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “打开电视,正在播放新闻节目”是必然事件 | |
| B. | “抛一枚硬币,正面向上的概率为$\frac{1}{2}$”表示每抛两次就有一次正面朝上 | |
| C. | “抛一枚均匀的正方体骰子,朝上的点数是6的概率为$\frac{1}{6}$”表示随着抛掷次数的增加,“抛出朝上的点数是6”这一事件发生的频率稳定在$\frac{1}{6}$附近 | |
| D. | 为了解某种节能灯的使用寿命,选择全面调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com