
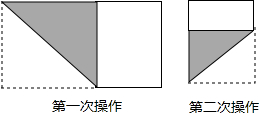
分析 根据操作步骤,可知每一次操作时所得正方形的边长都等于原矩形的宽.所以首先需要判断矩形相邻的两边中,哪一条边是矩形的宽.当$\frac{1}{2}$<a<1时,矩形的长为1,宽为a,所以第一次操作时所得正方形的边长为a,剩下的矩形相邻的两边分别为1-a,a.由1-a<a可知,第二次操作时所得正方形的边长为1-a,剩下的矩形相邻的两边分别为1-a,a-(1-a)=2a-1.由于(1-a)-(2a-1)=2-3a,所以(1-a)与(2a-1)的大小关系不能确定,需要分情况进行讨论.又因为可以进行三次操作,故分两种情况:①1-a>2a-1;②1-a<2a-1.对于每一种情况,分别求出操作后剩下的矩形的两边,根据剩下的矩形为正方形,列出方程,求出a的值.
解答 解:由题意,可知当$\frac{1}{2}$<a<1时,第一次操作后剩下的矩形的长为a,宽为1-a,所以第二次操作时正方形的边长为1-a,第二次操作以后剩下的矩形的两边分别为1-a,2a-1.
故答案为:1-a;
此时,分两种情况:
①如果1-a>2a-1,即a<$\frac{2}{3}$,那么第三次操作时正方形的边长为2a-1.
∵经过第三次操作后所得的矩形是正方形,
∴矩形的宽等于1-a,
即2a-1=(1-a)-(2a-1),解得a=$\frac{3}{5}$;
②如果1-a<2a-1,即a>$\frac{2}{3}$,那么第三次操作时正方形的边长为1-a.
则1-a=(2a-1)-(1-a),解得a=$\frac{3}{4}$.
故答案为:$\frac{3}{5}$或$\frac{3}{4}$.
点评 本题考查了一元一次方程的应用,解题的关键是分两种情况:①1-a>2a-1;②1-a<2a-1.分别求出操作后剩下的矩形的两边.


科目:初中数学 来源: 题型:填空题
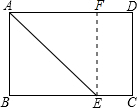 如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.
如图,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿AE对折,使得点B落在边AD上的点F处,折痕与边BC交于点E,则CE的长为2cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
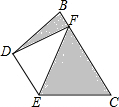 DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )
DE是△ABC的中位数,将△ADE沿DE所在的直线进行折叠,点A落在边BC的点F处,如图所示.若△DEF的面积为3,则图中阴影部分的面积为( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
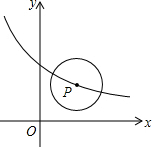 如图,⊙P的半径是1,圆心P在函数y=$\frac{3}{x+2}$(x>-2)的图象上运动,当⊙P与坐标轴相切时,圆心P的坐标为(1,1)或(-1,3).
如图,⊙P的半径是1,圆心P在函数y=$\frac{3}{x+2}$(x>-2)的图象上运动,当⊙P与坐标轴相切时,圆心P的坐标为(1,1)或(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16$\frac{9}{40}$米 | B. | $\frac{17}{4}$米 | C. | 16$\frac{7}{40}$米 | D. | $\frac{15}{4}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com