
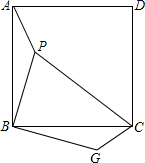
 如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.分析 (1)根据旋转的性质得出∠PBG=∠ABC=90°,BP=BP′即可证得△PBG是等腰直角三角形,从而求得PG=$\sqrt{2}$PB=2$\sqrt{2}$;
(2)根据勾股定理的逆定理即可求证.
解答 (1)解:∵∠ABP=∠CBG,
∴∠PBG=∠ABC=90°,
又∵BP=BG
∴△PBG是等腰直角三角形;
∴PG=$\sqrt{2}$PB=2$\sqrt{2}$;
(2)△PCG是直角三角形.
证明:∵PG=2$\sqrt{2}$,GC=PA=1,
∵(2$\sqrt{2}$)2+12=32
∴△PCG是直角三角形.
点评 本题主要考查了图形的旋转的性质以及勾股定理的逆定理,正确理解旋转中出现的相等的角和相等的边是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
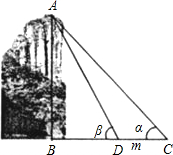 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).当α=44°,β=61°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).当α=44°,β=61°,m=50米时,求h的值.(精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7、 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com