
分析 先求得方程组的解,再由条件可列出关于m的不等式组,可求得m的取值范围.
解答 解:方程组$\left\{\begin{array}{l}{5x+2y=m+1①}\\{4x+y=m②}\end{array}\right.$,
②×2-①得:3x=m-1,
解得x=$\frac{m-1}{3}$,
把x=$\frac{m-1}{3}$代入②可得:4×$\frac{m-1}{3}$+y=m,
解得y=$\frac{4-m}{3}$,
∵x、y均小于1,
∴$\left\{\begin{array}{l}{\frac{m-1}{3}<1}\\{\frac{4-m}{3}<1}\end{array}\right.$,解得1<m<3,
∴m的取值范围为1<m<3.
点评 本题主要考查解方程组及不等式组的应用,利用加减消元法求得方程组的解是解题的关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:解答题
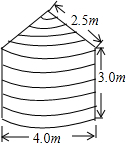 如图,要造一个粮仓,其上部是圆锥形,下部是圆柱形,如果每平方米需要用铁皮2m2(底部不用铁皮,接头忽略不计),那么按图中尺寸计算,一共需要多少平方米铁皮?(精确到0.1m2)
如图,要造一个粮仓,其上部是圆锥形,下部是圆柱形,如果每平方米需要用铁皮2m2(底部不用铁皮,接头忽略不计),那么按图中尺寸计算,一共需要多少平方米铁皮?(精确到0.1m2)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
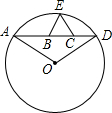 如图,A、D、E是⊙O上的三个点,且∠AOD=120°,B、C是弦AD上两点,BC=$\sqrt{3}$,△BCE是等边三角形.若设AB=x,CD=y,则y与x的函数关系式是y=$\frac{3}{x}$.
如图,A、D、E是⊙O上的三个点,且∠AOD=120°,B、C是弦AD上两点,BC=$\sqrt{3}$,△BCE是等边三角形.若设AB=x,CD=y,则y与x的函数关系式是y=$\frac{3}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
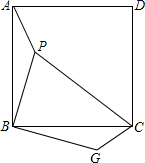 如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com