
分析 根据比赛盘数乘以每盘的得分,可得总得分,根据其余选手的得分,可得方程,根据选手数、得分都是整数,可得答案.
解答 解:设参赛的选手共有n+2人,除两人的(16分)外,其余n人平均得分为2k(k为整数),
所以n+2人总的分为16+2nk.
因为每人与其他人比赛一盘,
所以n+2人共赛了$\frac{(n+2)(n+1)}{2}$盘,而每盘比赛都得(2分),
故总得分为(n+2)(n+1)分,
从而有:16+2nk=(n+2)(n+1)化简得n(n+3-2k)=14
因为n,k均为正整数,
所以n可能为1,2,7,14,
又因为n为奇数,
故n=1,7,
当n=1时,n+3-2k=14得k=-5(舍去);当n=7时,k=4满足,所以共有9人参加比赛.
点评 此题考查了应用类问题,利用其余选手的得分得出方程是解题关键,又利用了因数、倍数的关系得出答案.


科目:初中数学 来源: 题型:解答题
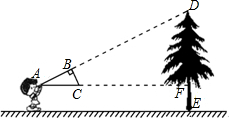 如图,小夏同学用自己做的直角三角形纸板ABC测量树的高度DE,小夏不断调整自己的位置,最终使纸板ABC的斜边AC保持水平,并且边AB与点D在同一直线上,已知纸板的两条直角边AB=0.4m,BC=0.2m,测得边AF=8m,AC离地面的高度为1.5m.求树高.
如图,小夏同学用自己做的直角三角形纸板ABC测量树的高度DE,小夏不断调整自己的位置,最终使纸板ABC的斜边AC保持水平,并且边AB与点D在同一直线上,已知纸板的两条直角边AB=0.4m,BC=0.2m,测得边AF=8m,AC离地面的高度为1.5m.求树高.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小刚 | B. | 小明 | C. | 同样大 | D. | 无法比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
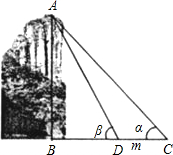 如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).当α=44°,β=61°,m=50米时,求h的值.(精确到1米)
如图,为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为α,前进m米至D处时测得峰顶A的仰角为β(此时C、D、B三点在同一直线上).当α=44°,β=61°,m=50米时,求h的值.(精确到1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com