
 如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )
如图,有一张面积为1的正方形纸片ABCD,M、N分别是AD,BC边上的中点,将点C折叠至MN上,落在P点的位置上,折痕为BQ,连PQ,则PQ的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 在Rt△PBN中由PB=2BN可求得∠PBN=60°,由翻折的性质可求得∠QBC=30°,PQ=CQ,在△BQC中由特殊锐角三角函数可求得QC=$\frac{\sqrt{3}}{3}$,从而求得PQ的长.
解答 解:∵M、N分别是AD,BC边上的中点,
∴∠PNB=90°,NB=$\frac{1}{2}$BP.
∴∠PBN=60°.
由翻折的性质可知:∠PBQ=∠CBQ=30°,PQ=CQ.
在Rt△BCQ中,$\frac{QC}{BC}=\frac{\sqrt{3}}{3}$,即$\frac{QC}{1}=\frac{\sqrt{3}}{3}$.
解得:QC=$\frac{\sqrt{3}}{3}$.
∴PQ=$\frac{\sqrt{3}}{3}$.
故选:B.
点评 本题主要考查的是翻折的性质、特殊锐角三角函数值,根据题意求得∠CBQ=30°是解题的关键.


科目:初中数学 来源:2017届江苏省东台市第四教育联盟九年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列运算正确的是( )
A. 3a+2a=a5 B. a2·a3=a6 C. (a+b)(a-b)=a2-b2 D. (a+b)2=a2+b2
查看答案和解析>>
科目:初中数学 来源:2015-2016学年内蒙古巴彦淖尔市临河区七年级下学期期末考试数学试卷(解析版) 题型:单选题
买钢笔和铅笔共30支,其中钢笔的数量比铅笔数量的2倍少3支.若设买钢笔x支,铅笔y支,根据题意,可得方程组( ).
A. 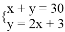
B. 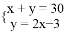
C. 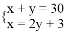
D. 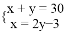
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
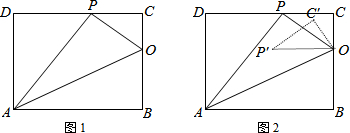
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
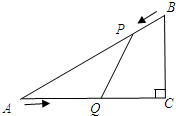 如图,已知在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:
如图,已知在Rt△ACB中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com