
【题目】如图,在平面直角坐标系中,A是抛物线y= ![]() x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,2),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
(1)当m= ![]() 时,求S的值.
时,求S的值.
(2)求S关于m(m≠2)的函数解析式.
(3)①若S= ![]() 时,求
时,求 ![]() 的值;
的值;
②当m>2时,设 ![]() =k,猜想k与m的数量关系并证明.
=k,猜想k与m的数量关系并证明.
【答案】
(1)
解:∵点A在二次函数y= ![]() x2的图象上,AE⊥y轴于点E,且AE=m,
x2的图象上,AE⊥y轴于点E,且AE=m,
∴点A的坐标为(m, ![]() m2),
m2),
当m= ![]() 时,点A的坐标为(
时,点A的坐标为( ![]() ,1),
,1),
∵点B的坐标为(0,2),
∴BE=OE=1.
∵AE⊥y轴,
∴AE∥x轴,
∴△ABE∽△CBO,
∴ ![]() =
= ![]() ,
,
∴CO=2 ![]() ,
,
∵点D和点C关于y轴对称,
∴DO=CO=2 ![]() ,
,
∴S= ![]() BEDO=
BEDO= ![]() ×1×2
×1×2 ![]() =
= ![]()
(2)
解:(i)当0<m<2时(如图1),
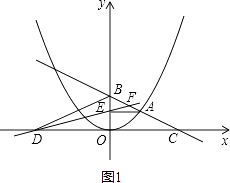
∵点D和点C关于y轴对称,
∴△BOD≌△BOC,
∵△BEA∽△BOC,
∴△BEA∽△BOD,
∴ ![]() ,即BEDO=AEBO=2m.
,即BEDO=AEBO=2m.
∴S= ![]() BEDO=
BEDO= ![]() ×2m=m;
×2m=m;
(ii)当m>2时(如图2),
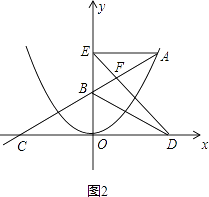
同(i)解法得:S= ![]() BEDO=
BEDO= ![]() AEOB=m,
AEOB=m,
由(i)(ii)得,
S关于m的函数解析式为S=m(m>0且m≠2).
(3)
解:①如图3,连接AD,

∵△BED的面积为 ![]() ,
,
∴S=m= ![]() ,
,
∴点A的坐标为( ![]() ,
, ![]() ),
),
∵ ![]() =
= ![]() =
= ![]() =k,
=k,
∴S△ADF=kS△BDF,S△AEF=kS△BEF,
∴ ![]() =
= ![]() =
= ![]() =k,
=k,
∴k= ![]() =
= ![]() =
= ![]() ;
;
②k与m之间的数量关系为k= ![]() m2,
m2,
如图4,连接AD,

∵ ![]() =
= ![]() =
= ![]() =k,
=k,
∴S△ADF=kS△BDF,S△AEF=kS△BEF,
∴ ![]() =
= ![]() =
= ![]() =k,
=k,
∵点A的坐标为(m, ![]() m2),S=m,
m2),S=m,
∴k= ![]() =
= ![]() =
= ![]() m2(m>2).
m2(m>2).
【解析】(1)首先可得点A的坐标为(m, ![]() m2),继而可得点E的坐标及BE、OE的长度,易得△ABE∽△CBO,利用对应边成比例求出CO,根据轴对称的性质得出DO,继而可求解S的值;(2)分两种情况讨论,(I)当0<m<2时,将BEDO转化为AEBO,求解;(II)当m>2时,由(I)的解法,可得S关于m的函数解析式;(3)①首先可确定点A的坐标,根据
m2),继而可得点E的坐标及BE、OE的长度,易得△ABE∽△CBO,利用对应边成比例求出CO,根据轴对称的性质得出DO,继而可求解S的值;(2)分两种情况讨论,(I)当0<m<2时,将BEDO转化为AEBO,求解;(II)当m>2时,由(I)的解法,可得S关于m的函数解析式;(3)①首先可确定点A的坐标,根据 ![]() =
= ![]() =
= ![]() =k,可得S△ADF=kS△BDFS△AEF=kS△BEF , 从而可得
=k,可得S△ADF=kS△BDFS△AEF=kS△BEF , 从而可得 ![]() =
= ![]() =
= ![]() =k,代入即可得出k的值;②可得
=k,代入即可得出k的值;②可得 ![]() =
= ![]() =
= ![]() =k,因为点A的坐标为(m,
=k,因为点A的坐标为(m, ![]() m2),S=m,代入可得k与m的关系.
m2),S=m,代入可得k与m的关系.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.
(1)若点P在线段CD上,如图1.
①依题意补全图1;
②判断AH与PH的数量关系与位置关系并加以证明;
(2)若点P在线段CD的延长线上,且∠AHQ=152°,正方形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD 是一段斜坡,AB 是水平线,现为了测斜坡上一点 D 的铅直高度(即 垂线段 DB 的长度),小亮在点 D 处立上一竹竿 CD,并保证 CD=AB,CD⊥AD,然后在竿顶 C 处垂下一根细绳(细绳末端挂一重锤,以使细绳与水平线垂直),细绳与斜坡 AD 交于点E,此时他测得 CE=8 m,AE=6 m,求 BD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气已经成为人们普遍关注的话题,雾霾不仅仅影响人们的出行,还影响着人们的健康,太原市会持续出现雾霾天气吗?在2016年2月周末休息期间,某校九年级1班综合实践小组的同学以“雾霾天气的主要成因”为主题,随机调查了太原市部分市民的观点,并对调查结果进行了整理,绘制了如下不完整的统计图表,观察并回答下列问题:
类别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 | m |
C | 城中村燃煤问题 | 15% |
D | 其他(绿化不足等) | n |
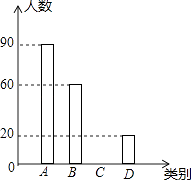
(1)请你求出本次被调查市民的人数及m,n的值,并补全条形统计图;
(2)若太原市有300万人口,请你估计持有A,B两类看法的市民共有多少人?
(3)学校要求小颖同学在A,B,C,D这四个雾霾天气的主要成因中,随机抽取两项作为课题研究的项目进行考察分析,请用画树状图或列表的方法,求出小颖同学刚好抽到B(汽车尾气排放),C(城中村燃煤问题)的概率.(用A,B,C,D表示各项目)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B两点,(点A在点B的左侧),与直线AC交于点C(2,3),直线AC与抛物线的对称轴l相交于点D,连接BD.
(1)求抛物线的函数表达式,并求出点D的坐标;
(2)如图2,若点M、N同时从点D出发,均以每秒1个单位长度的速度分别沿DA、DB运动,连接MN,将△DMN沿MN翻折,得到△D′MN,判断四边形DMD′N的形状,并说明理由,当运动时间t为何值时,点D′恰好落在x轴上?
(3)在平面内,是否存在点P(异于A点),使得以P、B、D为顶点的三角形与△ABD相似(全等除外)?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.
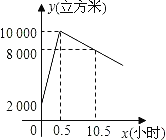
(1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气;
(2)当x≥0.5时,求储气罐中的储气量y(立方米)与时间x(小时)的函数解析式;
(3)请你判断,正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一条细绳系着一个小球在平面内摆动,已知细绳从悬挂点O到球心的长度为50厘米,小球在带你B位置时达到最低点,当小球在左侧点A时与最低点B时细绳相应所成的角度∠AOB=37°.(取sin37°=0.6,cos37°=0.8,tan37°=0.75) 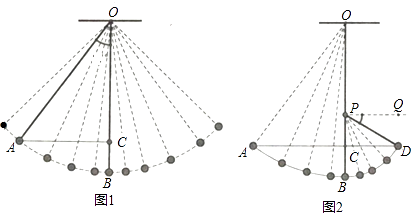
(1)求点A与点B的高度差BC的值.
(2)如图2,若在点O的正下方有一个阻碍物P,当小球从左往右落到最低处后,运动轨迹改变,变为以P为圆心,PB为半径继续向右摆动,当摆动至与点A在同一水平高度的点D时,满足PD部分细绳与水平线的夹角∠DPQ=30°,求OP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.

(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com