
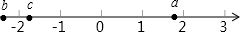 实数a、b、c在数轴上的对应点如图所示,其中|a|=|c|,化简|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c.
实数a、b、c在数轴上的对应点如图所示,其中|a|=|c|,化简|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c. 分析 根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.
解答 解:根据数轴上点的位置得:a>$\sqrt{2}$,b<-$\sqrt{3}$,c<-$\sqrt{2}$,
∴b+$\sqrt{3}$<0,c-$\sqrt{2}$<0,a-$\sqrt{2}$>0,
∵|a|=|c|,
∴a+c=0,
则原式=-b-$\sqrt{3}$+a-$\sqrt{2}$+$\sqrt{2}$-c+2c=a+c-b-$\sqrt{3}$=-b-$\sqrt{3}$.
点评 此题考查了实数的运算,以及实数与数轴,熟练掌握绝对值的代数意义是解本题的关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
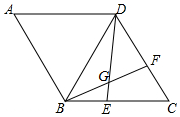 如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为2$\sqrt{7}$.
如图,在菱形ABCD中,AB=BD,点E,F分别在BC,CD边上,且CE=DF,BF与DE交于点G,若BG=2,DG=4,则CD长为2$\sqrt{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com