
分析 (1)根据题意可以求得x、y的值,从而可以求得xy的值;
(2)根据题意可以求得a、b的值,从而可以求得c的取值范围,由a、b、c都是正整数,从而可以求得c的最大值.
解答 解:(1)∵x2-2xy+2y2+6y+9=0,
∴(x2-2xy+y2)+(y2+6y+9)=0,
∴(x-y)2+(y+3)2=0,
∴x-y=0,y+3=0,
解得,x=3,y=-3,
∴xy=3×(-3)=-9;
(2)∵a2+b2-10a-12b+61=0,
∴(a2-10a+25)+(b2-12b+36)=0,
∴(a-5)2+(b-6)2=0,
∴a-5=0,b-6=0,
解得,a=5,b=6,
∴1<c<11,
∵△ABC的三边长a、b、c都是正整数,
∴c的最大值是10.
点评 本题考查因式分解的应用,偶数次方、三角形三边的关系,解答本题的关键是明确题意,找出所求问题需要的条件,利用偶数次方的性质和三角形三边的关系解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
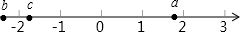 实数a、b、c在数轴上的对应点如图所示,其中|a|=|c|,化简|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c.
实数a、b、c在数轴上的对应点如图所示,其中|a|=|c|,化简|b+$\sqrt{3}$|+|a-$\sqrt{2}$|+|c-$\sqrt{2}$|+2c.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
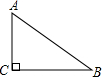 如图所示,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使点C为正方的一个顶点,其余三个顶点分别在AB、BC、AC上.
如图所示,△ABC是一块直角三角形余料,∠C=90°.工人师傅要把它加工成一个正方形零件,使点C为正方的一个顶点,其余三个顶点分别在AB、BC、AC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com