练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

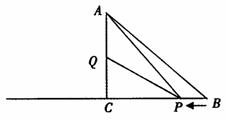
    如图，AC⊥CB，垂足为C点，AC＝CB＝8cm，点Q是AC的中点，动点P由B点出发，沿射线BC方向匀速移动．点P的运动速度为2cm/s.设动点P运动的时间为ts．为方便说明，我们分别记三角形ABC面积为，三角形PCQ的面积为，三角形PAQ的面积为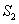，三角形ABP的面积为.

    (1) ＝    ㎝（用含t的代数式表示）；

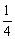
    (2)当点P运动几秒，＝，说明理由；

    (3)请你探索是否存在某一时刻，使得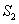＝＝，若存在，求出值，若不存在，说明理由．

    [来源:Z_xx_k.Com]


    （1）8t；

    （2）由题意，得当0≤t≤4时，，

    当t＞4时，，

    ∴当16-4t=×8×8×时，t=2，

    当4t-16=×8×8×时，t=6．

    答：当点P运动2秒或6秒时，＝；

    （3）由题意，得16-4t=8t，解得：t=．

    答：当t=时，＝＝．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    （2015•重庆）如图，在△ABD和△FEC中，点B，C，D，E在同一直线上，且AB=FE，BC=DE，∠B=∠E．求证：∠ADB=∠FCE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的方程2x+a-9=0的解是x=2，则a的值为

    A．2                      B．3                            C．4                            D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     有一个正六面体骰子（如图a）放在桌面上，将骰子沿如图所示的顺时针方向滚动，每滚动90°算一次，则滚动第2015次后，骰子朝下一面的点数是    ．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


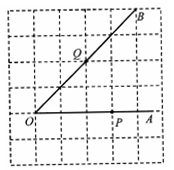
    如图，点P，Q分别是∠AOB的边OA，OB上的点．

    (1)过点P画OB的垂线，垂足为H；

    (2)过点Q画OA的垂线，交OA于点C，连接PQ；

    (3)线段QC的长度是点Q到      的距离，      的

    长度是点P到直线OB的距离，因为直线外一点和直线

    上各点连接的所有线段中，垂线段最短，所以线段PQ、

    PH的大小关系是          （用“＜”号连接）．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如右图，在Rt△ABC中，∠C=90°，AC=4，BC=3，则的值等于

        A．        B．       C．         D．

       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如右图，四边形ABCD内接于⊙O，E是BC延长线上一点，若∠BAD=105°，  则∠DCE的度数是          .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     在平面直角坐标系xOy中，已知两点A(0，3)，B(1，0)，现将线段AB绕点B按顺时针方向旋转90°得到线段BC，抛物线y=ax2+bx+c(a≠0)经过点C.

    （1）如图1，若该抛物线经过原点O，且.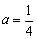

    ①求点C的坐标及该抛物线的表达式；

    ②在抛物线上是否存在点P，使得∠POB=∠BAO. 若存在，请求出所有满足条件的点P的坐标，若不存在，请说明理由；

    （2）如图2，若该抛物线y=ax2+bx+c(a≠0)经过点D(2，1)，点Q在抛物线上，且满足∠QOB=∠BAO. 若符合条件的Q点的个数是4个，请直接写出a的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，最大∠A是最小∠C的2倍，且AB＝2，AC＝3，则BC的长为       ．

    查看答案和解析>>

    同步练习册答案