
在平面直角坐标系xOy中,已知两点A(0,3),B(1,0),现将线段AB绕点B按顺时针方向旋转90°得到线段BC,抛物线y=ax2+bx+c(a≠0)经过点C.
(1)如图1,若该抛物线经过原点O,且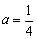 .
.
①求点C的坐标及该抛物线的表达式;
②在抛物线上是否存在点P,使得∠POB=∠BAO. 若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点D(2,1),点Q在抛物线上,且满足∠QOB=∠BAO. 若符合条件的Q点的个数是4个,请直接写出a的取值范围.

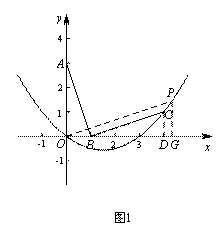
解:(1)①如图1,过点C作CD⊥x轴于点D.
∴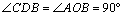 .
.
 ∵∠ABC=90º,
∵∠ABC=90º,
∴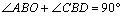 .
.
又∵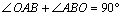 ,
,
∴ .
.
∵AB=BC,
∴△AOB≌△BDC.
∴BD=OA,CD=OB.
∵A(0,3),B(1,0),
∴C(4,1).
∵抛物线y=ax2+bx+c经过原点O,且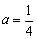 ,
,
∴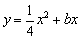 .
.
又∵抛物线经过点C(4,1),
∴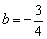 .
.
∴该抛物线的表达式为 .
.
② 当点P在第一象限时,过点P作PG⊥x轴于点G,连接OP.
∵∠POB=∠BAO,
∴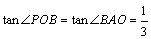 .
.
设P(3m,m),m>0.
∵点P在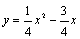 上,
上,
∴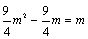 .
.
解得: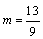 ,
,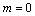 (舍去).
(舍去).
∴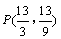 .
.
当点P在第四象限时,同理可求得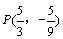 .
.
当点P在第二、三象限时,∠POB为钝角,不符合题意.
综上所述,在抛物线上存在使得∠POB=∠BAO的点P,点P的坐标为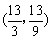 或
或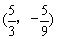 .
.
(2)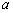 的取值范围为
的取值范围为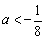 或
或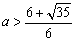 .
.


科目:初中数学 来源: 题型:
如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为ts.为方便说明,我们分别记三角形ABC面积为 ,三角形PCQ的面积为
,三角形PCQ的面积为 ,三角形PAQ的面积为
,三角形PAQ的面积为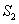 ,三角形ABP的面积为
,三角形ABP的面积为 .
.
(1)  = ㎝
= ㎝ (用含t的代数式表示);
(用含t的代数式表示);
(2)当点P运动几秒, =
=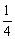
 ,说明理由;
,说明理由;
(3)请你探索是否存在某一时刻,使得 =
=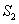 =
= ,若存在,求出
,若存在,求出 值,若不存在,说明理由.
值,若不存在,说明理由.
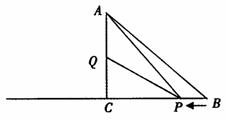
[来源:Z_xx_k.Com]
查看答案和解析>>
科目:初中数学 来源: 题型:
某校九年级进行集体跳绳比赛.如下图所示,跳绳时,绳甩到最高处时的形状可看作是某抛物线的一部分,记作G,绳子两端的距离AB约为8米,两名甩绳同学拿绳的手到地面的距离AC和BD基本保持1米,当绳甩过最低点时刚好擦过地面,且与抛物线G关于直线AB对称.
(1)求抛物线G的表达式并写出自变量的取值范围;
(2)如果身高为1.5米的小华站在CD之间,且距点C的水平距离为m米,绳子甩过最高处时超过她的头顶,直接写出m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的盒子里装有3个黑球和1个白球,每个球除颜色外都相同,从中任意摸出2个球,下列事件中,不可能事件是( )
A.摸出的2个球有一个是白球 B.摸出的2个球都是黑球
C.摸出的2个球有一个黑球 D.摸出的2个球都是白球
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com