
分析 已知x1、x2是一元二次方程2x2-2x+1-3m=0的两个实数根,可推出△=(-2)2-4×2(1-3m)≥0,根据根与系数的关系可得x1•x2=$\frac{1-3m}{2}$,x1+x2=1;且x1、x2满足不等式x1•x2+2(x1+x2)>0,代入即可得到一个关于m的不等式,由此可解得m的取值范围.
解答 解:∵方程2x2-2x+1-3m=0有两个实数根,
∴△=4-8(1-3m)≥0,解得m≥$\frac{1}{6}$.
由根与系数的关系,得x1+x2=1,x1•x2=$\frac{1-3m}{2}$.
∵x1•x2+2(x1+x2)>0,
∴$\frac{1-3m}{2}$+2>0,解得m<$\frac{5}{3}$.
∴$\frac{1}{6}$≤m<$\frac{5}{3}$.
故答案为:$\frac{1}{6}$≤m<$\frac{5}{3}$.
点评 本题考查了一元二次方程根的判别式:若方程有两个实数根,则△≥0,若方程没有实数根,则△<0.以及一元二次方程根与系数的关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
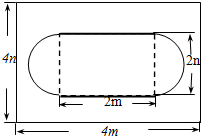 某居民小区为了美化环境,如图在一块长为4m,宽为4n的长方形绿地上建造花坛,花坛是由一个矩形和两个半圆组成的.求改造后剩下的绿地面积(π取3).
某居民小区为了美化环境,如图在一块长为4m,宽为4n的长方形绿地上建造花坛,花坛是由一个矩形和两个半圆组成的.求改造后剩下的绿地面积(π取3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
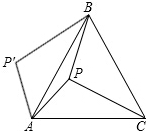 如图,P是等边△ABC内的一点,且PA=6,PB=8,若将△PAC绕点A逆时针旋转后,得到△P′AB,且∠APB=150°,则点P到P′之间的距离为6,PC=10.
如图,P是等边△ABC内的一点,且PA=6,PB=8,若将△PAC绕点A逆时针旋转后,得到△P′AB,且∠APB=150°,则点P到P′之间的距离为6,PC=10.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有一张长为8cm,宽为7cm的矩形纸片ABCD,现要剪下一个腰长为6cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为18或3$\sqrt{35}$或12$\sqrt{2}$cm2.
如图,有一张长为8cm,宽为7cm的矩形纸片ABCD,现要剪下一个腰长为6cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为18或3$\sqrt{35}$或12$\sqrt{2}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com