
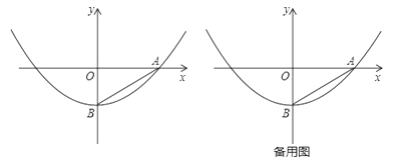
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�Rt��AOB��ֱ�DZ�OA��x���������ϣ�OB��y�Ḻ�����ϣ���OA=![]() ��OB=1���Ե�BΪ����������߾�����A��
��OB=1���Ե�BΪ����������߾�����A��
��1������������ߵĽ���ʽ��
��2���ڶ������ڵĵ�M���Ǿ���ԭ����ƽ��Rt��AOB�����ֱ����һ�㣮��OM=2�����жϵ�M�Ƿ��ڣ�1���е��������ϣ���˵�����ɣ�
��3����P�Ǿ�����B���������ƽ�е�ֱ��l��һ�㣮����̽������ֱ��l�Ƶ�B������ת������������ƽ�л��غϣ�ʱ���Ƿ����������ֱ��l����ֱ��l�����ҵ���P��ʹ��PAB��Rt��AOB���ƣ����ƱȲ�Ϊ1���������ڣ����ֱ��l�Ľ���ʽ���������ڣ�˵�����ɣ�
���𰸡���1��y=![]() x2��1��2����M����������y=
x2��1��2����M����������y=![]() x2��1�ϣ�3����������ֱ��l��y=��
x2��1�ϣ�3����������ֱ��l��y=��![]() x��1��y=��
x��1��y=��![]() x��1��y=
x��1��y=![]() x��1��������ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB����
x��1��������ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB����
��������
��1��������õ�A��B�����꣬����BΪ�����ߵĶ��㣬��������ߵĽ���ʽ����A����������a��ֵ������ȷ���������߽���ʽ��
��2����M�����������ϣ�����Ϊ������������x�����һ������ΪC��ֱ��OM��AB�ڵ�D��������õ�DΪAB���е㣬�õ�AD=OD=BD���õ���MON=��AOD=��OAD=30������MN��ֱ��OC�����MN��ON�ij���ȷ����M���꣬���������߽���ʽ���鼴�ɵõ������
��3�����ڣ���Rt��AOB�У�AO=![]() ��BO=1��AB=2����ABO=60�㣬��BAO=30����������������ǣ�������ABP=90��ʱ������AP1B=60��������ABP1�ס�AOB�������Ƶñ�����ȷ����P1�����꣬����B����ȷ����ֱ��l����ʽ���ɣ�������ABP=60��ʱ������BAP5=90��������ABP5�ס�OBA�������Ƶñ������P5���꣬ͬ��ȷ����ֱ��l����ʽ��������ABP=30����ֱ��l��AB�Ϸ�ʱ������P6AB=90��������ABP6�ס�OAB�������Ƶñ������P6���꣬ͬ��ȷ����ֱ��l����ʽ�����ϣ��õ�ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB����ʱ�����н���ʽ��
��BO=1��AB=2����ABO=60�㣬��BAO=30����������������ǣ�������ABP=90��ʱ������AP1B=60��������ABP1�ס�AOB�������Ƶñ�����ȷ����P1�����꣬����B����ȷ����ֱ��l����ʽ���ɣ�������ABP=60��ʱ������BAP5=90��������ABP5�ס�OBA�������Ƶñ������P5���꣬ͬ��ȷ����ֱ��l����ʽ��������ABP=30����ֱ��l��AB�Ϸ�ʱ������P6AB=90��������ABP6�ס�OAB�������Ƶñ������P6���꣬ͬ��ȷ����ֱ��l����ʽ�����ϣ��õ�ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB����ʱ�����н���ʽ��
��1��������ã�A��![]() ��0����B��0����1����
��0����B��0����1����
��BΪ�����ߵĶ��㣬
���������߽���ʽΪy=ax2��1��
��A�������ã�3a��1=0����a=![]() ��
��
�������߽���ʽΪy=![]() x2��1��
x2��1��
��2����M����������y=![]() x2��1�ϣ�����Ϊ��
x2��1�ϣ�����Ϊ��
����������x�����һ������ΪC��ֱ��OM��AB�ڵ�D����MN��OC�ڵ�N��
������ã�DΪAB���е㣬��OD=AD=BD��
���MON=��AOD=��OAD=30�㣬
��Rt��OMN��OM=2��
��MN=1��ON=![]() ����M����
����M����![]() ��1����
��1����
��y=![]() ������
������![]() ��2��1=0��1��
��2��1=0��1��
���M����������y=![]() x2��1�ϣ�
x2��1�ϣ�
��3�����ڣ���Rt��AOB�У�AO=![]() ��BO=1��AB=2����ABO=60�㣬��BAO=30�㣬
��BO=1��AB=2����ABO=60�㣬��BAO=30�㣬
������������ǣ�
�ٵ���ABP=90��ʱ������AP1B=60�㣬���ABP1�ס�AOB��
��![]() =
=![]() ����BP1=
����BP1=![]() =
=![]() ��
��
��OP1=![]() ����P1����
����P1����![]() ��0����[����Ҳ�������P2����
��0����[����Ҳ�������P2����![]() ��2����P3��
��2����P3��![]() ����2����P4��
����2����P4��![]() ����4��]��
����4��]��
��ֱ��l����ʽΪy=kx+b����B��P1�������ã�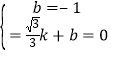 ��
��
��ã�![]() ��
��
��ʱֱ��l����ʽΪy=��![]() x��1��
x��1��
�ڵ���ABP=60��ʱ������BAP5=90�㣬���ABP5�ס�OBA��
��![]() =
=![]() ����BP5=
����BP5=![]() =4��
=4��
��P5��P5C��y���ڵ�G����Rt��BGP5�У���P5BG=60�㣬
��P5G=2![]() ��BG=2����P5��2
��BG=2����P5��2![]() ����3����
����3����
ͬ�����ֱ��l����ʽΪy=��![]() x��1��
x��1��
�۵���ABP=30����ֱ��l��AB�Ϸ�ʱ������P6AB=90�㣬���ABP6�ס�OAB��
��![]() =
=![]() ����BP6=
����BP6=![]() =
=![]() ��
��
��P6��P6H��y���ڵ�H����Rt��BP6H�У���P6BH=30�㣬
��P6H=![]() ��BH=2��
��BH=2��
��P6��![]() ��1����
��1����
ͬ���õ�ֱ��l����ʽΪy=![]() x��1��
x��1��
���ϣ���������ֱ��l��y=��![]() x��1��y=��
x��1��y=��![]() x��1��y=
x��1��y=![]() x��1��������ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB���ƣ�
x��1��������ֱ��l�����ҵ���P��ʹRt��PAB��Rt��AOB���ƣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����4������ֱ��������![]() �IJ�����Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊ
�IJ�����Ƭ�����dz����ֲ�ͬ������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊ![]() ������һ�������ȷֳ�4�ݵ�ת�̣�����ֱ��������
������һ�������ȷֳ�4�ݵ�ת�̣�����ֱ��������![]() ��ת��ת����ָ����ָ�����ּ�Ϊ
��ת��ת����ָ����ָ�����ּ�Ϊ![]() ����ָ��ָ�ڷָ�����������תһ�Σ������
����ָ��ָ�ڷָ�����������תһ�Σ������![]() ����������
����������![]() ��
��![]() ����Χ�ɵ������ڣ������߽磩�ĸ�����__________��
����Χ�ɵ������ڣ������߽磩�ĸ�����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪PΪ![]() ����ƽ����һ�㣬����PA��PB��PC����
����ƽ����һ�㣬����PA��PB��PC����![]() ��
��![]() ��
��![]() �У�������һ����������
�У�������һ����������![]() ����
����![]() ȫ�ȳ���
ȫ�ȳ���![]() ��ô�ͳ�PΪ
��ô�ͳ�PΪ![]() �Ĺ����Ƶ㡱���ݡ������Ƶ㡰�Ƿ����������ε��ڲ������ϻ��ⲿ���ɽ����Ϊ�ڹ����Ƶ㡱�����߹����Ƶ������Ƶ㡱��
�Ĺ����Ƶ㡱���ݡ������Ƶ㡰�Ƿ����������ε��ڲ������ϻ��ⲿ���ɽ����Ϊ�ڹ����Ƶ㡱�����߹����Ƶ������Ƶ㡱��
![]() �ݶ����֪���ȱ�������______
�ݶ����֪���ȱ�������______![]() ����ڡ�������
����ڡ�������![]() �����Ƶ�
�����Ƶ�
��̽�����ñ߹����Ƶ�̽�������ε���״
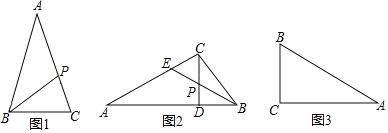
![]() ��ͼ1����
��ͼ1����![]() ��һ���߹����Ƶ�P����Խ����B�����ߣ���
��һ���߹����Ƶ�P����Խ����B�����ߣ���![]() �ָ�ɵ�����������ǡ��ԭ�����ξ����ƣ����ж�
�ָ�ɵ�����������ǡ��ԭ�����ξ����ƣ����ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��̽��2�����ڹ����Ƶ�̽�������ε��ڽǹ�ϵ
![]() ��ͼ2����
��ͼ2����![]() �У�
�У�![]() ������CD���ƽ����BE���ڵ�P����P��
������CD���ƽ����BE���ڵ�P����P��![]() ��һ���ڹ����Ƶ���˵����E��
��һ���ڹ����Ƶ���˵����E��![]() �ı߹����Ƶ㣬��ֱ��д��
�ı߹����Ƶ㣬��ֱ��д��![]() �Ķ�����
�Ķ�����
��̽����̽��ֱ�������ι����Ƶ�ĸ���
![]() ��ͼ3����
��ͼ3����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ���ԣ�������������P�㹲��______��
���ԣ�������������P�㹲��______��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��� mx2����m+2��x+2��0��
��1����֤����������ʵ������
��2��������������ʵ�������Ҷ�����������������mֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c�Ķ���M�ڵڶ����ޣ��Ҿ����� A(1��0)�͵� B(0��2)����
��1��a ��ȡֵ��Χ��________��
��2������AMO�����Ϊ��ABO�����![]() ��ʱ����a��ֵΪ________
��ʱ����a��ֵΪ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
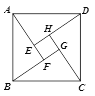
����Ŀ����ͼ���ҹ�������ѧ����ˬ��ע�⡶�����㾭��ʱ�����ġ���ˬ��ͼ����ͼ���ĸ�ֱ����������ȫ�ȵģ�����������ABCD�������С������EFGH�����13������![]() ��ֵΪ______________��
��ֵΪ______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��һ����Ȼ��1��2��3��k��ȥ������һ������ʣ�µ�����ƽ����Ϊ16����ȥ��������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һö���ػ���Ӿ��״�վC��5km�ĵ���O�����䣬����������A��Bʱ�����״�վC����õ�A��B�����Ƿֱ�Ϊ34�㣬45�������е�O��A��B��ͬһ��ֱ���ϣ���A��B�����ľ��루�����ȷ��0.1km����
���ο����ݣ�sin34��=0.56��cos34��=0.83��tan34��=0.67����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��һ����չ������������2014��������ij�ؼӴ��˽������ѵ�Ͷ�룬2014�����Ͷ���������6000��Ԫ��2016��Ͷ���������8640��Ԫ���������������Ͷ��������ѵ���ƽ����������ͬ��
��1�������������Ͷ��������ѵ���ƽ�������ʣ�
��2�������ؽ������ѵ�Ͷ�뻹��������ͬ����ƽ�������ʣ�����Ԥ��2017�����Ͷ��������Ѷ�����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com