
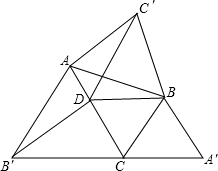
如图,△ABC中,∠ACB=60°,△ABC′,△BCA′,△CAB′都是△ABC形外的等边三角形,点D在边AC 上,且DC=BC.连接DB,DB′,DC′.有下列结论:
①CDB是等边三角形;
②△C′BD≌△B′DC;
③S△AC′D≠S△DB′A
④S△ABC+S△ABC′=S△ACB′+S△A′BC
其中,正确的结论有__________(请写序号,少选、错选均不得分)
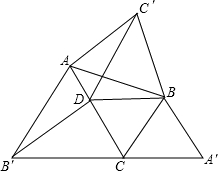
①②④
【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】根据等边三角形的性质得出△BCD是等边三角形以及∠C′BD=60°+∠ABD=∠ABC,进而证得△C′BD≌△ABC,△BCA≌△DCB′,进一步证得四边形AB′DC′是平行四边形,即可判断②③④.
【解答】解:∵BC=CD,∠ACB=60°,
∴△BCD是等边三角形,故①正确;
∵△ABC′和△BCD是等边三角形,
∴∠ABC′=∠DBC=60°,
∴∠C′BD=60°+∠ABD=∠ABC,
在△C′BD与△ABC中,
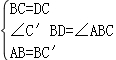 ,
,
∴△C′BD≌△ABC,
在△BCA与△DCB′中,

∴△BCA≌△DCB′(SAS).
∴△C′BD≌△B′DC,故②正确;
∵△C′BD≌△ABC,
∴∠C′DB=∠ACB=60°,C′D=AC,
∵∠DBC=60°,AB′=AC,
∴∠C′DB=∠DBC,C′D=AB′,
∴BC∥C′D,
∵∠AB′C=∠A′CB=60°,
∴BC∥A′B,
∴AB′∥DC′,
∴四边形AB′DC′是平行四边形,
∴S△AC′D=S△DB′A,故③错误;
∵S△AC′D=S△DB′A,S△B′CD=S△BC′D,
∴S△ABC+S△ABC′=S△ACB′+S△A′BC.故④正确.
故答案为①②④.
【点评】本题考查了等边三角形的判定和性质,全等三角形的判定和性质,平行四边形的判定和性质以及三角形面积等,熟练掌握性质定理是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
如图,点B,E,F,D在一条直线上,且DE=BF,点A,C在直线BD的两側,且AB=CD,AE=CF.连接AD,AF,CB,CE,则图中的全等三角形共有( )
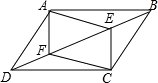
A.4对 B.5对 C.6对 D.7对
查看答案和解析>>
科目:初中数学 来源: 题型:
解不等式组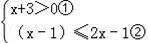

请结合题意填空,完成本题的解答
(Ⅰ)解不等式①,得
(Ⅱ)解不等式②,得
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为 .
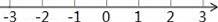

查看答案和解析>>
科目:初中数学 来源: 题型:
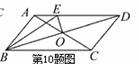
如图,在周长为20cm的▱ABCD中,AB≠AD,AC,BD相交于点O,OE⊥BD交AD于E,则△ABE的周长为( )
A.4 cm B.6 cm C.8 cm D.10 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com