
【题目】如图,在Rt△ABC中,∠B=90°,AB=20cm,BC=15cm,动点P从点A出发,以每秒4cm的速度沿AB方向运动,到达点B时停止运动.过点P作AB的垂线交斜边AC于点E,将△APE绕点P顺时针旋转90°得到△DPF.设点P在边AB上运动的时间为t(秒).

(1)当点F与点B重合时,求t的值;
(2)当△DPF与△ABC重叠部分的图形为四边形时,设此四边形的面积为S,求S与t的函数关系式;
(3)若点M是DF的中点,当点M恰好在Rt△ABC的内角角平分线上时,求t的值.
【答案】(1)![]() ;(2)S=
;(2)S=![]() (0<t≤
(0<t≤![]() );(3)
);(3)![]() 或
或![]() .
.
【解析】
(1)由条件可得AP=4t,易证![]() ,根据相似三角形的性质可得PE=3t,由旋转的性质可得PE= PF,然后根据PF+AP=AB建立方程,就可求出t的值.
,根据相似三角形的性质可得PE=3t,由旋转的性质可得PE= PF,然后根据PF+AP=AB建立方程,就可求出t的值.
(2)先用t的代数式表示出DE长及![]() 的面积,然后证明
的面积,然后证明![]() ,再求出
,再求出![]() 的面积,然后运用相似三角形性质(相似三角形的面积比等于相似比的平方)将
的面积,然后运用相似三角形性质(相似三角形的面积比等于相似比的平方)将![]() 的面积用t的代数式表示,就可得到S与t的函数关系式.
的面积用t的代数式表示,就可得到S与t的函数关系式.
(3)设DF交AC于点G,过点M作MH⊥AB于点H,过点M作MN⊥BC于点N,如图3,先分别用t的代数式表示出MG、MH、MN的长,然后运用角平分线的性质建立等量关系,就可求出t的值.
(1) ∵△APE绕点P顺时针旋转90°得到△DPF,
∴∠D=∠A,∠DFP=∠AEP,∠DPB=∠APE=90°,AP=DP,EP=FP,AE=DF,
∵点F与点B重合,
∴PB=PF,
∴EP=BP,
∵AB=20,AP=4t,
∴EP=BP=20-4t,
∵∠APE=∠ABC=90°,
∴PE∥BC,
∴![]() ,
,
∴![]() ,
,
∵BC=15,AP=4t,AB=20,
∴PE=3t,
∵EP=BP=20-4t,
∴3t=10-4t,
解得:t=![]() ,
,
∴t的值为![]() (秒);
(秒);
(2)当![]() 与
与![]() 重叠部分的图形为四边形时,如下图:
重叠部分的图形为四边形时,如下图:
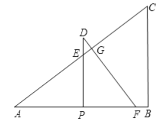
此时0<t≤![]() ,
,
∵PE∥BC,
∴∠DEG=∠C,
又∵∠D=∠A,
∴![]() ,
,
∴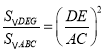 ,
,
∵∠B=90°,AB=20,BC=15,
∴AC=25, ![]() =
=![]() =150,
=150,
∵DE=DP-EP=AP-EP=4t-3t=t,
∴![]() ,
,
∴![]() =
=![]() ,
,
∵![]() =
=![]() =
=![]() =
=![]() ,
,
∴S=![]() -
-![]() =
=![]() -
-![]() =
=![]() ,
,
∴S与t的函数关系式为:S=![]() (0<t≤
(0<t≤![]() ).
).
(3)设DF交AC于点G,过点M做MH⊥AB于点H,过点M作MN⊥BC于点N,如下图:
∵![]() ,
,
∴∠DGE=∠B=90°, ![]() ,
,
∵DE=t,AB=20,AC=25,
∴DG=![]() ,
,
∵∠APE=90°,AP=4t,PE=3t,
∴AE=5t,
∴DF=AE=5t,
∵点M是DF的中点,
∴DM=FM=![]() DF=
DF=![]() ,
,
∴MG=DM-DG=![]() =
=![]() ,
,
∵∠MHF=∠DPF=90°,
∴MH∥DP,
∴![]() ,
,
∴![]() ,
,
∴MH=![]() DP=2t,FH=
DP=2t,FH=![]() FP=
FP=![]() EP=
EP=![]() ,
,
∴HB=AB-AP-PH=20-4t-![]() =20-
=20-![]() ,
,
∵∠MHB=∠B=∠MNB=90°,
∴四边形MNBH为矩形,
∴MN=HB=20-![]() ,
,
①当点M在∠A的角平分线上时,
∵MG⊥AC,MH⊥AB,
∴MG=MH,
∴![]() =2t,
=2t,
解得:t=0(舍去).
②当点M在∠B的角平分线上时,
∵MN⊥BC,MH⊥AB,
∴MH=MN,
∴2t=20- ![]() ,
,
解得:t= ![]() ,
,
③当点M在∠C的角平分线上时,
∵MG⊥AC,MN⊥BC,
∴MG=MN,
∴![]() =20-
=20- ![]() ,
,
解得:t= ![]() ,
,
综上所述,当点M恰好在![]() 的内角角平分线上时,t的值为
的内角角平分线上时,t的值为![]() (秒)或
(秒)或![]() (秒).
(秒).


科目:初中数学 来源: 题型:
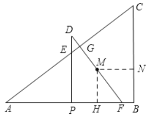
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴只有一个公共点
轴只有一个公共点![]() ,且与
,且与![]() 轴交于点
轴交于点![]()
(1)试判断该抛物线的开口方向,说明理由;
(2)若![]() ,
,![]() 轴交该抛物线于点
轴交该抛物线于点![]() ,且
,且![]() 是直角三角形,求抛物线的解析式;
是直角三角形,求抛物线的解析式;
(3)若直线![]() (
(![]() )与该抛物线有两个交点,且与
)与该抛物线有两个交点,且与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,记
,记![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,提高学生的综合素质,促进中学生全面发展,学校开展了多种社团活动.小明喜欢的社团有:合唱社团、足球社团、书法社团、科技社团(分别用字母A,B,C,D依次表示这四个社团),并把这四个字母分别写在四张完全相同的不透明的卡片的正面上,然后将这四张卡片背面朝上洗匀后放在桌面上.
(1)小明从中随机抽取一张卡片是足球社团B的概率是 .
(2)小明先从中随机抽取一张卡片,记录下卡片上的字母后不放回,再从剩余的卡片中随机抽取一张卡片,记录下卡片上的字母.请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,点E为AB的中点.
(1)求证:△ADC∽△ACB.
(2)若AD=2,AB=3,求![]() 的值.
的值.
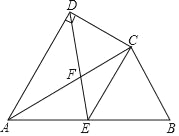
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】娄底市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套150平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送三年物业管理费.物业管理费为每平方米每月1.5元.请问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线y=kx+3与
中,直线y=kx+3与![]() 轴、
轴、![]() 轴分别相交于点A、B,并与抛物线
轴分别相交于点A、B,并与抛物线![]() 的对称轴交于点
的对称轴交于点![]() ,抛物线的顶点是点
,抛物线的顶点是点![]() .
.
(1)求k和b的值;
(2)点G是![]() 轴上一点,且以点
轴上一点,且以点![]() 、C、
、C、![]() 为顶点的三角形与△
为顶点的三角形与△![]() 相似,求点G的坐标;
相似,求点G的坐标;
(3)在抛物线上是否存在点E:它关于直线AB的对称点F恰好在y轴上.如果存在,直接写出点E的坐标,如果不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在梯形ABCD中,![]() ,P是线段BC上一点,以P为圆心,PA为半径的
,P是线段BC上一点,以P为圆心,PA为半径的![]() 与射线AD的另一个交点为Q,射线PQ与射线CD相交于点E,设
与射线AD的另一个交点为Q,射线PQ与射线CD相交于点E,设![]() .
.
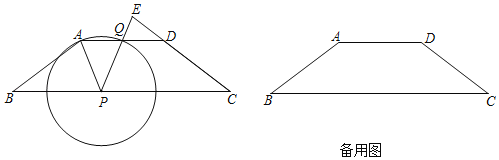
(1)求证:![]() ;
;
(2)如果点Q在线段AD上(与点A、D不重合),设![]() 的面积为y,求y关于x的函数关系式,并写出定义域;
的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果![]() 与
与![]() 相似,求BP的长.
相似,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com