
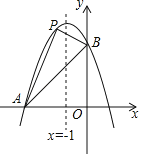
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)△PAB的面积的最大值为![]() ,此时点P的坐标(
,此时点P的坐标(![]() ,
,![]() ).
).
【解析】
(1)因为对称轴是直线x=-1,所以得到点A(-3,0)的对称点是(1,0),因此利用交点式y=a(x-x1)(x-x2),求出解析式.
(2)根据面积的和差,可得二次函数,根据二次函数的性质,可得最大值,根据自变量与函数值的对应关系,可得答案.
(1)∵抛物线对称轴是直线x=﹣1且经过点A(﹣3,0)
由抛物线的对称性可知:抛物线还经过点(1,0)
设抛物线的解析式为y=a(x﹣x1)(x﹣x2)(a≠0)
即:y=a(x﹣1)(x+3)
把B(0,3)代入得:3=﹣3a
∴a=﹣1
∴抛物线的解析式为:y=﹣x2﹣2x+3.
(2)设直线AB的解析式为y=kx+b,
∵A(﹣3,0),B(0,3),
∴![]() ,
,
∴直线AB为y=x+3,
作PQ⊥x轴于Q,交直线AB于M,
设P(x,﹣x2﹣2x+3),则M(x,x+3),
∴PM=﹣x2﹣2x+3﹣(x+3)=﹣x2﹣3x,
∴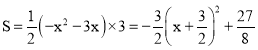 ,
,
当![]() 时,
时,![]() ,
, ,
,
∴△PAB的面积的最大值为![]() ,此时点P的坐标为(
,此时点P的坐标为(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.

(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=60°,∠B=75°,则:∠C= °,∠D= °;
(2)已知,如图2,在平面直角坐标系xOy中,四边形ABCD是等对角四边形,其中A(﹣2,0),C(2,0),B(-1,![]() ),点D在y轴上.
),点D在y轴上.
①若抛物线y=ax2+bx+c过点A,C,D,求二次函数的解析式;
②若抛物线y=ax2+bx+c(a<0)过点A,C,点P在抛物线上,当满足∠APC=![]() ∠ADC的P点至少有3个时,总有不等式2n﹣
∠ADC的P点至少有3个时,总有不等式2n﹣![]()
![]() +
+![]() 成立,求n的取值范围.
成立,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )

A. 1B. ![]() C. 2D. 4
C. 2D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好数学的甲、乙两个同学做了一个数字游戏:拿出三张正面写有数字﹣1,0,1且背面完全相同的卡片,将这三张卡片背面朝上洗匀后,甲先随机抽取一张,将所得数字作为p的值,然后将卡片放回并洗匀,乙再从这三张卡片中随机抽取一张,将所得数字作为q值,两次结果记为![]() .
.
(1)请你帮他们用树状图或列表法表示![]() 所有可能出现的结果;
所有可能出现的结果;
(2)求满足关于x的方程![]() 没有实数根的概率.
没有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箱子里有4瓶牛奶,其中有一瓶是过期的.现从这4瓶牛奶中不放回地任意抽取2瓶.
(1)请用树状图或列表法把上述所有等可能的结果表示出来;
(2)求抽出的2瓶牛奶中恰好抽到过期牛奶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
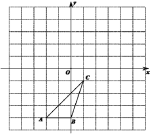
【题目】如图,△ABC的顶点坐标分别为A(-2,-4),B(0,-4),C(1,-1).
(1)画出△ABC关于点O的中心对称图形△A1B1C1.
(2)画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为 .
(3)若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为 .(用含m,n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=20cm,BC=15cm,动点P从点A出发,以每秒4cm的速度沿AB方向运动,到达点B时停止运动.过点P作AB的垂线交斜边AC于点E,将△APE绕点P顺时针旋转90°得到△DPF.设点P在边AB上运动的时间为t(秒).

(1)当点F与点B重合时,求t的值;
(2)当△DPF与△ABC重叠部分的图形为四边形时,设此四边形的面积为S,求S与t的函数关系式;
(3)若点M是DF的中点,当点M恰好在Rt△ABC的内角角平分线上时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
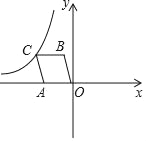
【题目】如图A(﹣4,0),B(﹣1,3),以OA、OB为边作OACB,经过A点的一次函数y=k1x+b与反比例函数y=![]() 的图象交于点C.
的图象交于点C.
(1)求一次函数y=k1x+b的解析式;
(2)请根据图象直接写出在第二象限内,当k1x+b>![]() 时,自变量x的取值范围;
时,自变量x的取值范围;
(3)将OACB向上平移几个单位长度,使点A落在反比例函数的图象上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com