
【题目】如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )

A. 1B. ![]() C. 2D. 4
C. 2D. 4
【答案】C
【解析】
如图,延长FH交AB于点M,由BE=2AE,DF=2FC,G、H分别是AC的三等分点,证明EG//BC,FH//AD,进而证明△AEG∽△ABC,△CFH∽△CAD,进而证明四边形EHFG为平行四边形,再根据平行四边形的面积公式求解即可.
如图,延长FH交AB于点M,
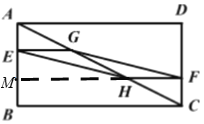
∵BE=2AE,DF=2FC,AB=AE+BE,CD=CF+DF,
∴AE:AB=1:3,CF:CD=1:3,
又∵G、H分别是AC的三等分点,
∴AG:AC=CH:AC=1:3,
∴AE:AB=AG:AC,CF:CD=CH:CA,
∴EG//BC,FH//AD,
∴△AEG∽△ABC,△CFH∽△CDA,BM:AB=CF:CD=1:3,∠EMH=∠B,
∴EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,
∵四边形ABCD是矩形,AB=3,BC=6,
∴CD=AB=3,AD=BC=6,∠B=90°,
∴AE=1,EG=2,CF=1,HF=2,BM=1,
∴EM=3-1-1=1,EG=FH,
∴EG![]() FH,
FH,
∴四边形EHFG为平行四边形,
∴S四边形EHFG=2×1=2,
故选C.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
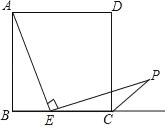
【题目】如图,在边长为3的正方形ABCD中,点E是BC边上的点,EC=2,∠AEP=90°,且EP交正方形外角的平分线CP于点P,则PC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,AC为对角线,∠DAC=∠BCA,且AD=BC,CD⊥AD于点D。
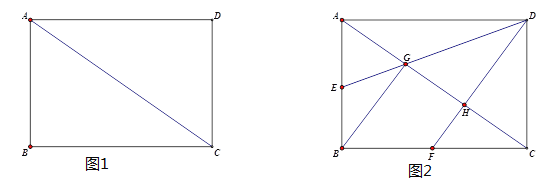
(1)如图1,求证:四边形ABCD是矩形。
(2)如图2,点E和点F分别为边AB和边BC的中点,连接DE、DF分别交AC于点G和点H,连接BG,在不连接其它线段的情况下,请写出所有面积是△FHC面积的2倍的所有三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
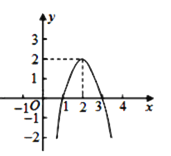
(1)写出方程ax2+bx+c=0的两个根;
(2)写出y随x的增大而减小的自变量x的取值范围;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电商时代使得网购更加便捷和普及.小张响应国家号召,自主创业,开了家淘宝店.他购进一种成本为100元/件的新商品,在试销中发现:销售单价x(元)与每天销售量y(件)之间满足如图所示的关系.
(1)求y与x之间的函数关系式;
(2)若某天小张销售该产品获得的利润为1200元,求销售单价x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,
OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的![]() ,那么点B′的坐标是【 】
,那么点B′的坐标是【 】
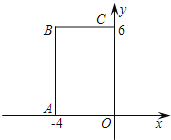
A.(-2,3) B.(2,-3) C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
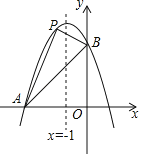
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】娄底市某楼盘准备以每平方米5000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望.为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4050元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套150平方米的房子.开发商还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送三年物业管理费.物业管理费为每平方米每月1.5元.请问哪种方案更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com