
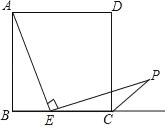
【题目】如图,在边长为3的正方形ABCD中,点E是BC边上的点,EC=2,∠AEP=90°,且EP交正方形外角的平分线CP于点P,则PC的长为_____.
【答案】![]()
【解析】
在AB上取BN=BE,连接EN,根据已知及正方形的性质利用ASA判定△ANE≌△ECP,从而得到NE=CP,在等腰直角三角形BNE中,由勾股定理即可解决问题.
在AB上取BN=BE,连接EN,作PM⊥BC于M.

∵四边形ABCD是正方形,∴AB=BC,∠B=∠DCB=∠DCM=90°.
∵BE=BN,∠B=90°,∴∠BNE=45°,∠ANE=135°.
∵PC平分∠DCM,∴∠PCM=45°,∴∠ECP=135°.
∵AB=BC,BN=BE,∴AN=EC.
∵∠AEP=90°,∴∠AEB+∠PEC=90°.
∵∠AEB+∠NAE=90°,∴∠NAE=∠PEC,∴△ANE≌△ECP(ASA),∴NE=CP.
∵BC=3,EC=2,∴NB=BE=1,∴NE=![]() =
=![]() ,∴PC=
,∴PC=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
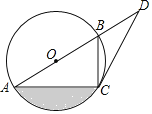
【题目】如图,已知AB是⊙O上的点,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
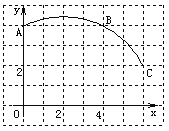
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请回答:
(1)该圆弧所在圆心D点的坐标为 ;
(2)扇形DAC的圆心角度数为 ;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的高.(保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程
(1)x2-7x+6=0
(2)(5x-1)2=3(5x-1)
(3) x2-4x-3=0 (用配方法)
(4) x2+4x+2=0(用公式法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+ax+b与x轴交于点A(﹣1,0),B(3,0).
(1)求抛物线的解析式;
(2)过点D(0,![]() )作x轴的平行线交抛物线于E,F两点,求EF的长;
)作x轴的平行线交抛物线于E,F两点,求EF的长;
(3)当![]() 时,直接写出x的取值范围是 .
时,直接写出x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
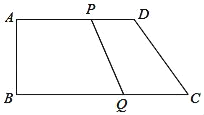
【题目】如图,在在四边形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线段AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动,当P点到达D点时,动点P、Q同时停止运动,设点P、Q同时出发,并运动了t秒,回答下列问题:
(1)BC= cm;
(2)当t= 秒时,四边形PQBA成为矩形.
(3)是否存在t,使得△DQC是等腰三角形?若存在,请求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
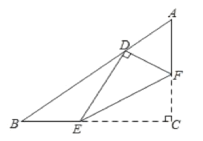
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.

(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=60°,∠B=75°,则:∠C= °,∠D= °;
(2)已知,如图2,在平面直角坐标系xOy中,四边形ABCD是等对角四边形,其中A(﹣2,0),C(2,0),B(-1,![]() ),点D在y轴上.
),点D在y轴上.
①若抛物线y=ax2+bx+c过点A,C,D,求二次函数的解析式;
②若抛物线y=ax2+bx+c(a<0)过点A,C,点P在抛物线上,当满足∠APC=![]() ∠ADC的P点至少有3个时,总有不等式2n﹣
∠ADC的P点至少有3个时,总有不等式2n﹣![]()
![]() +
+![]() 成立,求n的取值范围.
成立,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )

A. 1B. ![]() C. 2D. 4
C. 2D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com