
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.

(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=60°,∠B=75°,则:∠C= °,∠D= °;
(2)已知,如图2,在平面直角坐标系xOy中,四边形ABCD是等对角四边形,其中A(﹣2,0),C(2,0),B(-1,![]() ),点D在y轴上.
),点D在y轴上.
①若抛物线y=ax2+bx+c过点A,C,D,求二次函数的解析式;
②若抛物线y=ax2+bx+c(a<0)过点A,C,点P在抛物线上,当满足∠APC=![]() ∠ADC的P点至少有3个时,总有不等式2n﹣
∠ADC的P点至少有3个时,总有不等式2n﹣![]()
![]() +
+![]() 成立,求n的取值范围.
成立,求n的取值范围.
【答案】(1)150,75;(2)①y=﹣![]() x2+2;②n≤
x2+2;②n≤![]() .
.
【解析】
(1)∠A≠∠C,∠A=60°,∠B=75°,则∠B=75°=∠D,四边形的内角和为360°,故∠C=150°,即可求解;
(2)①证明△ACD为等腰直角三角形,故点D(0,2),即可求解;
②以D(0,2)为圆心,AD长为半径作⊙D,以D’(0,-2)为圆心,AD长为半径作⊙D’,如图所示,⊙D交y轴正半轴于点E,⊙D′交y轴负半轴于点F,当点P在优弧AEC和优弧AFC上时,∠APC=![]() ∠ADC,当抛物线过E点时满足题意的P点有3个,即可求解.
∠ADC,当抛物线过E点时满足题意的P点有3个,即可求解.
(1)∠A≠∠C,∠A=60°,∠B=75°,则∠B=75°=∠D,
四边形的内角和为360°,故∠C=150°,
故答案为:150,75;
(2)①如图2,过点B作BH⊥x轴于点H,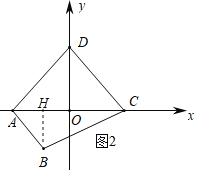
则AH=OH=1,BH=![]() ,HC=3,
,HC=3,
故tan∠HAB=![]() =tan∠HBC,
=tan∠HBC,
则∠BAH=∠CHB=60°,∴∠ABC=90°,
而∠DAO=∠DCO,∠CAB=60°,∠BCA=30°,
∴∠DAB≠∠DCB,故∠ADC=∠ABC=90°,
故△ACD为等腰直角三角形,故点D(0,2),
则抛物线的表达式为:y=ax2+2,
将点A的坐标代入上式并解得:a=-![]() ,
,
故抛物线的表达式为:y=-![]() x2+2;
x2+2;
②∵A(-2,0)、C(2,0)、B(-1,-![]() ),
),
∴AB=2,BC=2![]() ,AC=4,
,AC=4,
∴AB2+BC2=AC2,∴∠ABC=90°,
∵AD=CD,AB≠BC,
∴∠BAD≠∠BCD,
∵四边形ABCD是“等对角四边形”
∴∠ADC=∠ABC=90°,∴D(0,2)
∵抛物线y=ax2+bx+c过点A、C,
∴y=a(x+2)(x-2)=ax2-4a,
即:a=-![]() c,令t=2c2+16a-8
c,令t=2c2+16a-8![]() ,
,
则t=2c2-4c-8![]() ,
,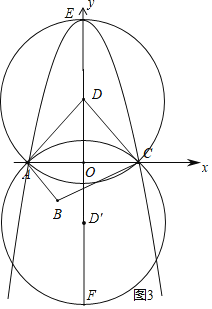
以D(0,2)为圆心,AD长为半径作⊙D,以D′(0,-2)为圆心,AD长为半径作⊙D′,
如图所示,⊙D交y轴正半轴于点E,⊙D′交y轴负半轴于点F.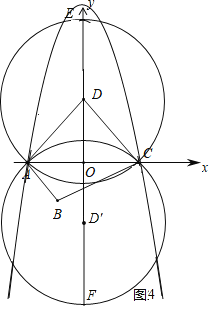
当点P在优弧AEC和优弧AFC上时,∠APC=![]() ∠ADC,当抛物线过E点时满足题意的P点有3个,
∠ADC,当抛物线过E点时满足题意的P点有3个,
此时,c=OE=OD+ED=2+2![]() ,
,
当满足∠APC=![]() ∠ADC的P点至少有3个时,c≥2+2
∠ADC的P点至少有3个时,c≥2+2![]() ,
,
当c≥2+2![]() 时,t=2c2-4c-8
时,t=2c2-4c-8![]() ≥16,
≥16,
∵总有不等式2n-![]() ≤2c2+16a-8
≤2c2+16a-8![]() 成立
成立
∴2n-![]() ≤16,
≤16,
解得:n≤![]() .
.


科目:初中数学 来源: 题型:
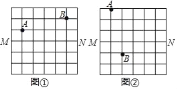
【题目】图①、图②均是8×8的正方形网格,每个小正方形的顶点称为格点,点A、B、M、N均落在格点上,在图①、图②给定的网格中按要求作图.
(1)在图①中的格线MN上确定一点P,使PA与PB的长度之和最小
(2)在图②中的格线MN上确定一点Q,使∠AQM=∠BQM.
要求:只用无刻度的直尺,保留作图痕迹,不要求写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
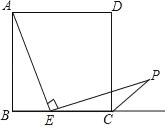
【题目】如图,在边长为3的正方形ABCD中,点E是BC边上的点,EC=2,∠AEP=90°,且EP交正方形外角的平分线CP于点P,则PC的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(定义)从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,△ABC中,∠A=40°,∠B=60°,CD平分∠ACB.求证:CD为△ABC的完美分割线;
(2)在△ABC中,CD是△ABC的完美分割线,其中△ACD为等腰三角形,设∠A=x°,∠B=y°,则y与x之间的关系式为_____________________________;
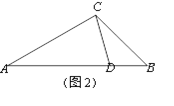
(3)如图2,△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市创全国卫生城市,某街道积极响应,决定在街道内的所有小区安装垃圾分类的温馨提示牌和垃圾箱,若购买4个垃圾箱比购买5个温馨提示牌多350元,垃圾箱的单价是温馨提示牌单价的3倍.
![]() 求温馨提示牌和垃圾箱的单价各是多少元?
求温馨提示牌和垃圾箱的单价各是多少元?
![]() 如果该街道需购买温馨提示牌和垃圾箱共3000个.
如果该街道需购买温馨提示牌和垃圾箱共3000个.
![]() 求购买温馨提示牌和垃圾箱所需费用
求购买温馨提示牌和垃圾箱所需费用![]() 元
元![]() 与温馨提示牌的个数x的函数关系式;
与温馨提示牌的个数x的函数关系式;
![]() 若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的
若该街道计划费用不超过35万元,而且垃圾箱的个数不少于温馨提示牌的个数的![]() 倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元?
倍,求有几种可供选择的方案?并找出资金最少的方案,求出最少需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,AC为对角线,∠DAC=∠BCA,且AD=BC,CD⊥AD于点D。
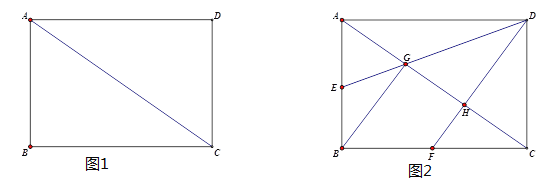
(1)如图1,求证:四边形ABCD是矩形。
(2)如图2,点E和点F分别为边AB和边BC的中点,连接DE、DF分别交AC于点G和点H,连接BG,在不连接其它线段的情况下,请写出所有面积是△FHC面积的2倍的所有三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
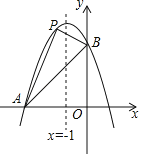
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com