练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，和，分别平分和，与相交于点，若，，则等于(　　)

    A.B.C.D.

    【答案】C

    【解析】

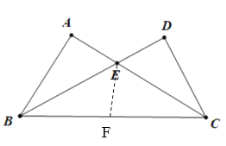
    在BC上截取BF=AB, 连接EF,易证，△ABE≌△FBE(SAS), △DCE≌△FCE(SAS),得出∠EFC=∠D=, ∠A=∠EFB=180°-89°=91°，设∠ABE=x，由三角形的内角和定理得到方程，求解可得答案.

    解：在BC上截取BF=AB，连接EF,

    ∵

    ∴DC=FC

    ∵分别平分和,

    ∴△ABE≌△FBE(SAS), △DCE≌△FCE(SAS),

    ∴∠EFC=∠D=, ∠A=∠EFB=180°-89°=91°

    ∴∠A-∠D=2°

    又∠AEB=∠CED,

    ∴∠ABE=∠DCE-2°

    设∠ABE=x，则∠ABC=2x, ∠EBC=x, ∠DCB=2x+4°

    在△BCD中，∠EBC+∠DCB+∠D=180°，

    即x+2x+4°+89°=180°

    解得x=29°

    ∴∠ABC=2x=58°,

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：四边形ABCD中，AC为对角线，∠DAC＝∠BCA，且AD＝BC，CD⊥AD于点D。

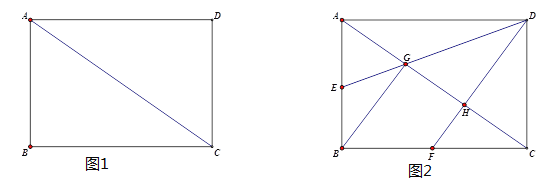
    （1）如图1，求证：四边形ABCD是矩形。

    （2）如图2，点E和点F分别为边AB和边BC的中点，连接DE、DF分别交AC于点G和点H，连接BG，在不连接其它线段的情况下，请写出所有面积是△FHC面积的2倍的所有三角形。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

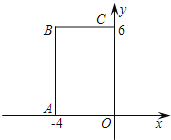
    【题目】 如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，

    OC在y轴上，如果矩形OA′B′C′与矩形OABC关于点O位似，且矩形OA′B′C′的面积等于矩形OABC面积的，那么点B′的坐标是【 】

    A．（－2，3） B．（2，－3） C．（3，－2）或（－2，3） D．（－2，3）或（2，－3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

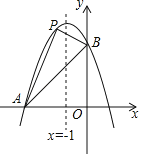
    【题目】如图，已知抛物线经过两点A（﹣3，0），B（0，3），且其对称轴为直线x＝﹣1．

    （1）求此抛物线的解析式；

    （2）若点P是抛物线上点A与点B之间的动点（不包括点A，点B），求△PAB的面积的最大值，并求出此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

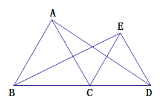
    【题目】如图，点C为线段BD上的一点，△ABC和△CDE是等边三角形.

    （1）求证：AD=BE.

    （2）以点C为中心，将△CDE逆时针方向旋转，旋转角为ɑ(0°＜ɑ＜360°).

    ①当ɑ为多少时DE∥AB?直接写出结果，不要求证明.

    ②当BC=6, CD=4时 ,设点E到直线AB的距离为y, 当ɑ为多少时，点E到直线AB的距离最小？求出最小值，并简洁说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线与轴只有一个公共点，且与轴交于点

    (1)试判断该抛物线的开口方向，说明理由；

    (2)若，轴交该抛物线于点，且是直角三角形，求抛物线的解析式；

    (3)若直线()与该抛物线有两个交点，且与轴和轴分别交于点，记的面积为，求的取值范围

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了丰富校园文化生活，提高学生的综合素质，促进中学生全面发展，学校开展了多种社团活动．小明喜欢的社团有：合唱社团、足球社团、书法社团、科技社团（分别用字母A，B，C，D依次表示这四个社团），并把这四个字母分别写在四张完全相同的不透明的卡片的正面上，然后将这四张卡片背面朝上洗匀后放在桌面上．

    （1）小明从中随机抽取一张卡片是足球社团B的概率是　 　．

    （2）小明先从中随机抽取一张卡片，记录下卡片上的字母后不放回，再从剩余的卡片中随机抽取一张卡片，记录下卡片上的字母．请你用列表法或画树状图法求出小明两次抽取的卡片中有一张是科技社团D的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】娄底市某楼盘准备以每平方米5000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望.为了加快资金周转，房地产开发商对价格经过两次下调后，决定以每平方米4050元的均价开盘销售.

    (1)求平均每次下调的百分率；

    (2)某人准备以开盘均价购买一套150平方米的房子.开发商还给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，送三年物业管理费.物业管理费为每平方米每月1.5元.请问哪种方案更优惠？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是的直径，弦，

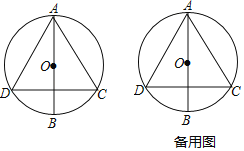
    （1）求证：是等边三角形．

    （2）若点是的中点，连接，过点作，垂足为，若，求线段的长；

    （3）若的半径为4，点是弦的中点，点是直线上的任意一点，将点绕点逆时针旋转60°得点，求线段的最小值．

    查看答案和解析>>

    同步练习册答案