
【题目】下面的图形是由边长为l的正方形按照某种规律排列而组成的.
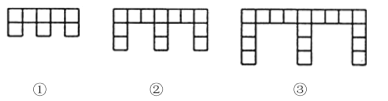
(1)观察图形,填写下表:

(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为![]() .
.
【答案】(1)13,28,18,38;(2)5n+3,10n+8;(3)y=2x+2
【解析】
(1)先数出图形中正方形的个数,再根据正方形的个数算出图形的周长;
(2)根据题(1)中的表格结果,归纳出规律,再以此类推至第n个图形中的情况;
(3)根据题(2)中的结论,即可得出y与x之间的关系.
(1)观察图形,可数出第2个图形中正方形的个数为13个,周长为28
第3个图形中正方形的个数为18,周长为38;
(2)观察题(1)的表格可发现:
第1个图形中,正方形有8个,即![]() ,周长是18,即
,周长是18,即![]()
第2个图形中,正方形有13个,即![]() ,周长是28,即
,周长是28,即![]()
第3个图形中,正方形有18个,即![]() ,周长是38,即
,周长是38,即![]()
由此推测第n个图形中,正方形的个数为:![]() ,周长为:
,周长为:![]() ;
;
(3)根据题(2)可知,第n个图形中,![]()
整理得:![]()
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

(1)求证:AE与⊙O相切;
(2)当BC=4,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在解一元二次方程时,发现有这样一种解法:
如:解方程x(x+4)=6.
解:原方程可变形,得:[(x+2)﹣2][(x+2)+2]=6.
(x+2)2﹣22=6,
(x+2)2=6+22,
(x+2)2=10.
直接开平方并整理,得.x1=﹣2+![]() ,x2=﹣2﹣
,x2=﹣2﹣![]() .
.
我们称小明这种解法为“平均数法”.
(1)下面是小明用“平均数法”解方程(x+3)(x+7)=5时写的解题过程.
解:原方程可变形,得:[(x+a)﹣b][(x+a)+b]=5.
(x+a)2﹣b2=5,
(x+a)2=5+b2.
直接开平方并整理,得.x1=c,x2=d.
上述过程中的a、b、c、d表示的数分别为 , , , .
(2)请用“平均数法”解方程:(x﹣5)(x+3)=6.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织275名师生郊游,计划租用甲、乙两种客车共7辆,已知甲客车载客量是30人,乙客车载客量是45人,其中,每辆乙种客车租金比甲种客车多100元,5辆甲种客车和2辆乙种客车租金共需3000元.
(1)租用一辆甲种客车、一辆乙种客车的租金各多少元?
(2)设租用甲种客车![]() 辆,总租车费为
辆,总租车费为![]() 元,求
元,求![]() 与
与![]() 的函数关系式;在保证275名师生都有座位的前提下,求当租用甲种客车多少辆时,总租车费最少,并求出这个最少费用.
的函数关系式;在保证275名师生都有座位的前提下,求当租用甲种客车多少辆时,总租车费最少,并求出这个最少费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系![]() 中,正比例函数
中,正比例函数![]() 与一次函数
与一次函数![]() 的图象相交于点
的图象相交于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
轴的垂线,分别交正比例函数的图像于点B,交一次函数的图象于点C,连接OC.
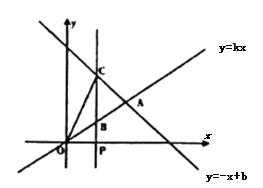
(1)求这两个函数解析式.
(2)求![]() 的面积.
的面积.
(3)在坐标轴上存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形,请直接写出
为腰的等腰三角形,请直接写出![]() 点的坐标。
点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com