
【题目】快车与慢车分别从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留![]() ,然后按原路原速返回,快车与慢车晚
,然后按原路原速返回,快车与慢车晚![]() 到达甲地.快慢两车距各自出发地的路程
到达甲地.快慢两车距各自出发地的路程![]() 与所用的时间
与所用的时间![]() 的关系如图所示.
的关系如图所示.

(1)甲乙两地之间的路程为_________________![]() ;快车的速度为_________________
;快车的速度为_________________![]() ;慢车的速度为______________
;慢车的速度为______________![]() ;
;
(2)出发________________![]() ,快慢两车距各自出发地的路程相等;
,快慢两车距各自出发地的路程相等;
(3)快慢两车出发______________![]() 相距
相距![]() .
.
【答案】(1)420,140,70;(2)![]() ;(3)
;(3)![]() h或
h或![]() h或
h或![]() h相距250km
h相距250km
【解析】
(1)先得两地的距离,根据速度=路程÷时间列式计算即可求出快车和慢车的速度;
(2)根据两车的速度得出B,D,E点坐标,进而得出设BD和OE直线解析式,进而得出交点坐标横坐标即可得出答案;
(3)分别根据两车相遇以及两车相遇后两车距离为250km时,列方程可解答.
解:(1)由图可知:甲乙两地之间的路程为420km;
快车的速度为:![]() =140km/h;
=140km/h;
由题意得:快车7小时到达甲地,则慢车6小时到达甲地,
则慢车的速度为:![]() =70km/h;
=70km/h;
故答案为:420,140,70;
(2)∵快车速度为:140km/h,
∴A点坐标为;(3,420),
∴B点坐标为(4,420),
可得E点坐标为:(6,420),D点坐标为:(7,0),
∴设BD解析式为:y=kx+b
![]()
解得:![]()
∴BD解析式为:y=-140x+980,
设OE解析式为:y=ax,
∴420=6a,
解得:a=70,
∴OE解析式为:y=70x,
当快、慢两车距各自出发地的路程相等时:70x=-140x+980,
解得:x=![]() ,
,
答:出发![]() 小时,快、慢两车距各自出发地的路程相等;
小时,快、慢两车距各自出发地的路程相等;
故答案为:![]() ;
;
(3)第一种情形第一次没有相遇前,相距250km,
则140x+70x+250=420,
解得:x=![]() ,
,
第二种情形应是相遇后而快车没到乙地前140x+70x-420=250,
解得:x=![]() ,
,
第三种情形是快车从乙往甲返回:70x-140(x-4)=250,
解得:x=![]() ,
,
综上所述:快慢两车出发![]() h或
h或![]() h或
h或![]() h相距250km.
h相距250km.


科目:初中数学 来源: 题型:
【题目】(本题满分14分)如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.

(1)求证:AE⊥BF;
(2)若OA-OB=1,求OA的长及四边形OECF的面积;
(3)连接OD,若△AOD是以AD为腰的等腰三角形,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某饮品店老板新推出A、B两种囗味的饮料,其中每杯A种口味饮料的利润率为60%,每杯B种口味饮料的利润率为20%.当售出的A种口味的杯数比B种口味的杯数少50%时,这个老板得到的总利润率为36%;当售出的A种口味的杯数比B种口味的杯数多25%时,这个老板得到的总利润率为_____.(利润率=利润÷成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天到了,鲜花盛开,人们都喜欢用美丽的花朵装点家庭,北碚花市生意兴隆,某花店老板三月份购进一批山茶花、绣球花共1000株,进价均为每株42元,山茶花以每株80元、绣球花以每株64元的价格销售.
(1)若要求三月份的总获利至少33200元,问该老板至少应购进山茶花多少株?
(2)四月份绣球花品种丰富、花型饱满,在进价不变的情况下,该老板决定调整价格,将山茶花的价格在三月份的基础上下调a%(降价后售价不低于进价),绣球花的价格上调![]() a%,同时山茶花的销量较三月份最低利润时销量下降了
a%,同时山茶花的销量较三月份最低利润时销量下降了![]() a%,绣球花的销量较月份最低利润时销量上升了40%,结果四月份的销售额比三月份最低利润时增加了3520元,求a的值.
a%,绣球花的销量较月份最低利润时销量上升了40%,结果四月份的销售额比三月份最低利润时增加了3520元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一场暴雨过后,一洼地存雨水20米 3,如果将雨水全部排完需 t分钟,排水量为 a米 3/分,且排水时间为5~10分钟
(1)试写出 t与 a的函数关系式,并指出 a的取值范围;
(2)请画出函数图象
(3)根据图象回答:当排水量为3米 3/分时,排水的时间需要多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
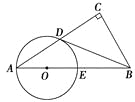
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买![]() 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台![]() 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台![]() 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买![]() 两种设备的方案;
两种设备的方案;
(2)已知每台![]() 型设备价格为3万元,每台
型设备价格为3万元,每台![]() 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com